anglhorairearcsemidiurneplanincline

Angle horaire du cercle horaire passant par l'intersection

d'un arc semi-diurne

avec le plan d'un cadran solaire incliné

Jean Pakhomoff

Chapitre 3

Les cadrans inclinés inclinants

Heures utiles.

fig 10

Considérons l'arc semi-diurne R'R'' de déclinaison d. L'arc R'R représente la portion cachée de cet arc semi-diurne.
Rappelons que, en gnomonique, les azimuts et les angles horaires sont comptés de 0 à 180° du

sud au nord en est comme en ouest.
Le triangle sphérique S’SUw rectangle en S permet d'écrire en appelant j le côté S’S:

tg j / tg (pi/2 – i) = sin (pi/2 - dg)
ou encore tg j = cos dg / tg i de même tg SUw / tg SS’Uw = sin j ou encore

tg (pi/2 - dg) / tg SS’Uw = sin j et tg SS’Uw = 1 / (tg dg sin j)
PS’R = SS’Uw (angles opposés)

Le triangle sphérique S’PR dans lequel PS’ = pi/2 - f + pi/2 – j = pi – (f + j) et PR = pi/2 – d

(f étant la latitude et d la déclinaison du soleil)
permet d'écrire sin PS’R / cos d = sin (pi - R) / sin (j + f) = sin (t) / sin S’R et sin S’R = sin t sin (j + f) / sin R
de même
sin R = sin PS’R sin (j + f) / cos d'où R.Lorsque R se trouve dans la zone sous équatoriale où les déclinaisons sont négatives

on aura PR= pi/2 + abs (d) et sin (pi/2+ abs(d)) = cos d donc aucun changement pour sin R (on peut même entrer d avec son signe
puisque cos d = cos - d). voir la fig 4 a

Quand R = pi/2 cos d = sin SS'Uw sin (f + j) ce qui nous donne d que nous appellerons dl dans ce cas particulier.
1) j < pi/2 – f (fig 17)
;
d décroît de M en S’ et pi - R croît de M en S’ donc R décroît de M en S'; on en déduit que lorsque d > dl_ R est > pi/2 et

nous retiendrons la plus grande valeur donnée par sin R. Inversement si d < dl alors R < pi/2
1) j > pi/2 – f (fig 17 a)

d croît de M en S’ et pi – R croît également. R décroît donc.

On en déduit que lorsque d < dl , R est > pi/2 et nous retiendrons la plus grande valeur donnée par sin R. Ce sera l’inverse pour d > dl.
Nous avons donné plus haut une autre méthode d'appréciation pour la valeur de R donnée par sin R: pour les inclinants on aura

fig 11
Appelons dm la déclinaison du point M.
pour j < pi/2 – f (fig 17) on a PM = pi/2 - dm = PN + NM = f + j et dm = pi/2 – (f + j)
pour j > pi/2 – f (fig 17 a) on a PM = pi/2 - (-dm) = PN + NM = f + j d’où - dm = pi/2 – (f + j)
R va se déplacer de M en S’ ce qui correspond à un intervalle de déclinaisons égal à dm = abs (pi/2 – (f + j))
Les déclinaisons comprises entre dm et - dm sont celles des arcs diurnes coupant l’incliné.

Donc les déclinaisons compatibles avec des apparitions disparitions seront comprises entre dm et – dm.
On écrira que si abs (d) > dm alors d est incompatible avec des passages diurnes sur le plan du cadran.

Il faudra alors choisir une autre déclinaison. Cette condition sera valable que j soit > ou < que pi/2 - f.
De même dans S’PR on a cos S’R = cos S’P cos PR + sin S’P sin PR cos (t) et

cos S’R = cos (pi -(j + f)) sin d + sin (j + f) cos d cos ( t)
ou cos S’R = -cos (j + f) sin d + sin (j + f) cos d cos ( t) rappel:
sin (pi – t) = sin t et cos (pi – t) = - cos t

cos PS’ = cos S’R cos PR + sin S’R sin PR cos (pi -R)

= cos S’R cos PR - sin S’R sin PR cos R

en remplaçant cos MR et sin MR par leurs valeurs on obtient

cos PS’ = -cos (j + f) sin² d + sin (j + f) cos d sin d cos (t) - sin S’R sin PR cos R cos PS’ =

cos (pi -(j + f)) =
-cos (j + f) = -cos (j + f) sin² d + sin (j + f) cos d sin d cos (t) - (sin t sin (j + f) cos d cos R) / sin R
Divisons le tout par cos (j + f)

-1 = - sin² d + tg (j + f) cos d sin d cos t - sin t tg (j + f) cos d / tg R et
–cos² d - tg (j + f) cos d sin d cos (t) + sin t tg (j + f) cos d / tg R = 0 Divisons par cos d
-cos d - tg (j + f) sin d cos (t) + sin t tg (j + f) / tg R = 0

En posant A = -cos d, B = - tg (j + f) sin d et C = + tg (j + f) / tg R

on a A + B cos t + C sin t = 0
Nous nous servons des propriétés de l'arc moitié en posant tg (t/2) = k on a alors

cos t = (1 – k²) / (1 + k²) et sin t = 2 k / (1 + k²)
et A + B (1 – k²) / (1 + k²) + C 2 k / (1 + k²) = 0

A + A k² + B - B K² + 2 C k = 0 et (A – B) k² + 2 kC + A + B = 0

Equation du second degré admettant 2 racines dont nous choisirons la racine la plus proche du résultat attendu.

Voyons maintenant les iIWLE

Lignes Est de l’aprés-midi. C’est ce que nous nommons iIWLE.

Heures utiles.

Fig 12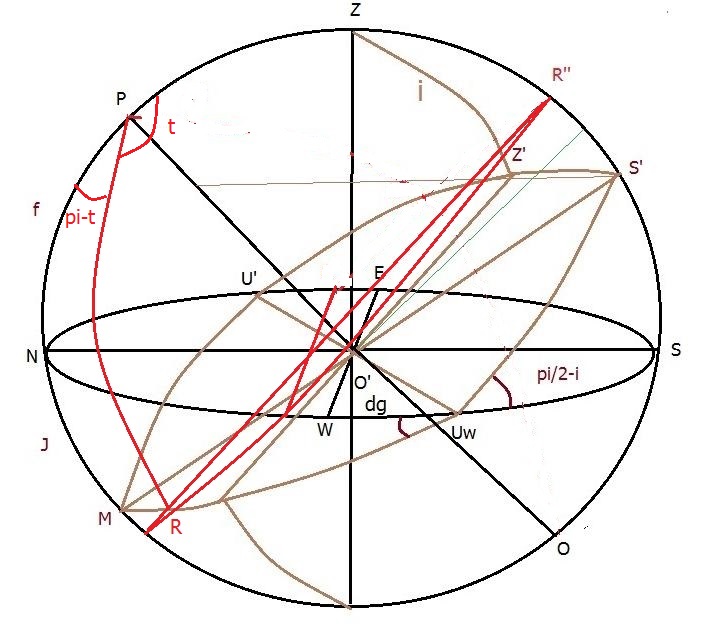 INCL19

La figure ci-dessus montre l'intersection de l'arc semi-diurne avec le plan du cadran en R l'astre étant couché.
Pas de changement en ce qui concerne le calcul de j mais il nous faut considérer ici le triangle sphérique S’PR dans lequel

PS’R = pi – SS’UW
On a vu précédemment que tg SS’Uw = 1 / (tg dg sin j)

Dans ce triangle sphérique S’PR on a également PS’ = pi/2 - f + pi/2 – j = pi – (f + j) et PR = pi/2 – d

(f étant la latitude et d la déclinaison du soleil)
permet d'écrire sin PS’R / cos d = sin (pi - R) / sin (j + f) = sin (t) / sin S’R

et sin S’R = sin t sin (j + f) / sin R de même sin R = sin PS’R sin (j + f) / cos d

= sin SS’UW sin (j + f) / cos d d'où R.
Lorsque R se trouve dans la zone sous équatoriale où les déclinaisons sont négatives on aura

PR= pi/2 + abs (d) et sin (pi/2+ abs(d)) = cos d donc aucun changement pour sin R (on peut même entrer d avec son signe
puisque cos d = cos - d).

Quand R = pi/2 cos d = sin SS'Uw sin (f + j) ce qui nous donne d que nous appellerons dl dans ce cas particulier.
1) j < pi/2 – f (fig 14)

d décroît de M en S’ et pi-R croît d'où R décroît de M en S’ on en déduit que lorsque d > dl _R est > pi/2 et nous retiendrons la

plus grande valeur donnée par sin R. Inversement si d < dl alors R < pi/2
2) j > pi/2 – f (fig 15)

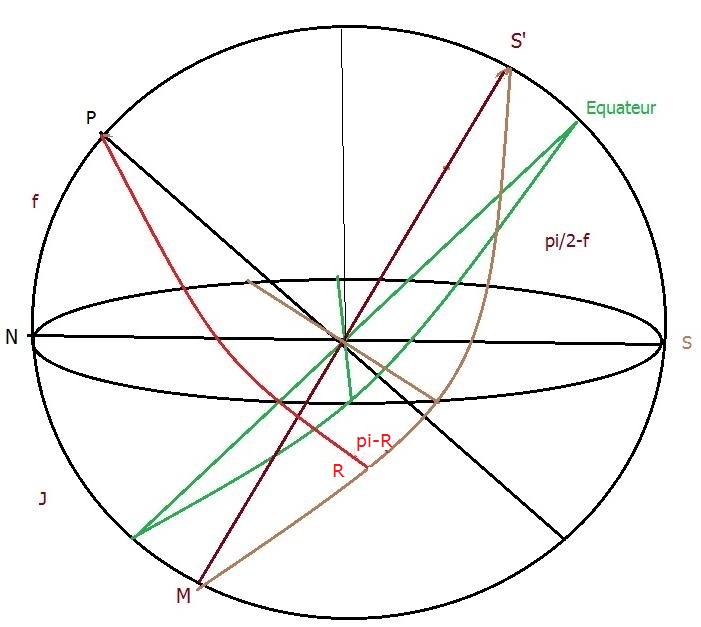
fig 13
d croît de M en S’ et pi - R croît de M en S’ donc R décroît de M en S': on en déduit que lorsque d < dl alors R est > pi/2 et

nous retiendrons la plus grande valeur donnée par sin R.
Ce sera l’inverse pour d > dl.
Appelons dm la déclinaison du point M.

pour j < pi/2 – f (fig 19) on a PM = pi/2 - dm = PN + NM = f + j et

dm = pi/2 – (f + j)

pour j > pi/2 – f (fig 19 a) on a PM = pi/2 - (-dm) = PN + NM = f + j d’où - dm = pi/2 – (f + j)
R va se déplacer de M en S’ ce qui correspond à un intervalle de déclinaisons égal à dm = abs (pi/2 – (f + j))
Les déclinaisons comprises entre dm et - dm sont celles des arcs diurnes coupant l’incliné.

Il faudra alors choisir une autre déclinaison. Cette condition sera valable que j soit > ou < pi/2 - f.
De même cos S’R = cos S’P cos PR + sin S’P sin PR cos (t) et cos S’R = cos (pi -(j + f)) sin d + sin (j + f) cos d cos (t)
(sin PR = sin (pi/2 + abs (d)) = cos abs (d) = cos d)

ou cos S’R = -cos (j + f) sin d + sin (j + f) cos d cos ( t) rappel:
sin (pi – t) = sin t et cos (pi – t) = - cos t

cos PS’ = cos S’R cos PR + sin S’R sin PR cos (pi -R) cos PS’ = cos S’R cos PR - sin S’R sin PR cos R
en remplaçant cos MR et sin MR par leurs valeurs on obtient

cos PS’ = -cos (j + f) sin² d + sin (j + f) cos d sin d cos (t) - sin S’R sin PR cos R cos PS’ = cos (pi -(j + f)) =
-cos (j + f) = -cos (j + f) sin² d + sin (j + f) cos d sin d cos (t) - (sin t sin (j + f) cos d cos R) / sin R
Divisons le tout par cos (j + f)

-1 = - sin² d + tg (j + f) cos d sin d cos t - sin t tg (j + f) cos d / tg R et
---- cos² d - tg (j + f) cos d sin d cos (t) + sin t tg (j + f) cos d / tg R = 0 Divisons par cos d
-cos d - tg (j + f) sin d cos (t) + sin t tg (j + f) / tg R = 0

En posant A = - cos d, B = - tg (j + f) sin d et C = + tg (j + f) / tg R
on a A + B cos t + C sin t = 0 Même relation que pour les INWLW
Les deux racines de l'équation donneront les heures d'apparition et de disparition du

soleil sur le plan du cadran.

A propos des heures utiles pour les iIE nous pourrions nous dispenser de calculs car par

similitude avec les résultats précédemment obtenus on doit pouvoir accepter sans réticence

que les relation cherchées sont encore identiques à celles des iIWLW et iIWLE.

On adaptera alors l'attribution des racines au cas envisagé.

Vérifions cela dans le cas des IELW (symétrique des IWLE vu ci-dessus).

Vérifions cela rapidement pour les IELW (symétrique des IWLE vu ci-dessus).

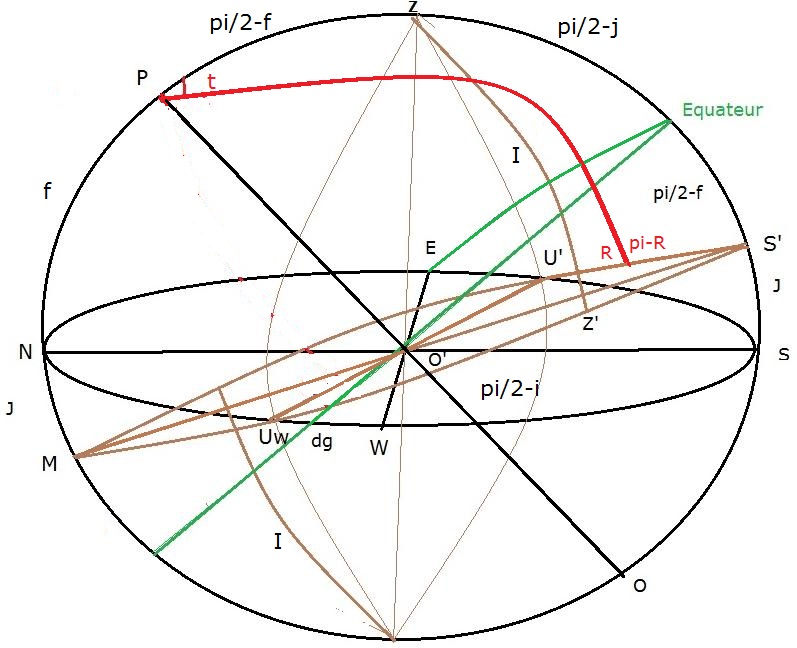
fig 14
On considère le triangle PS'R même calcul pour SS'U' et PS'U' = PS'R = pi – SS'U'
sin PS'R / cos d = sin (pi – R) / sin (f+j) = sin t / sin S'R et sin S'R=sin t sin (j+f) / sin R
de même sin (pi – R) = sin R = sin PS'R sin (j + f) / cos d d'où R.

Lorsque j < pi/2 – f, d décroît avec R en allant de M à S' donc si d>dl, R>pi/2

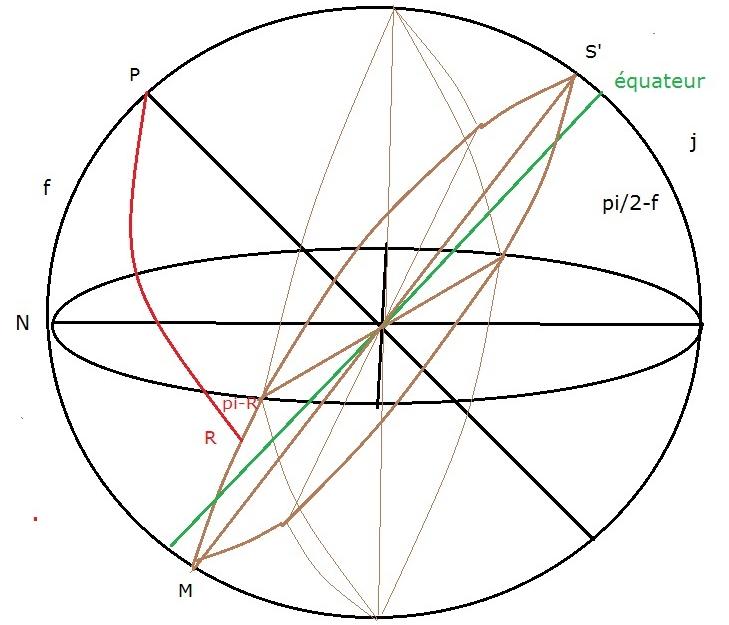
fig 15
quand j > pi/2 – f:
Mêmes calculs pour R d croît de M en S' alors que pi-R croît et R décroît
donc si d<dl alors R>pi/2 donc mêmes résultats que pour les IW
pareil pour
abs (d) > dm alors d est incompatible avec des passages diurnes sur le plan du cadran.
voir la suite
De même dans MPR on a cos MR =…….

cos S'R = cos (pi - (j + f)) sin d + sin (pi - (j + f)) cos d cos t
(sin PR = sin (pi/2 + abs (d)) = cos abs (d) = cos d)

ou cos S'R = - cos (j + f) sin d + sin (j + f) cos d cos (t) rappel:
sin (pi – t) = sin t et cos (pi – t) = - cos t

cos PS' = cos S'R cos PR + sin S'R sin PR cos (pi – R) =
cos S'R cos PR - sin S'R sin PR cos R
en remplaçant cos MR et sin MR par leurs valeurs … le reste des calculs est identique au cas des IWLE.

On utilisera donc les mêmes relations dans le programme informatique.

Retour chapitre 1

Retour chapitre 2

Les cadrans inclinés

Les cadrans solaires de Jean Pakhomoff

Travaux personnels en gnomonique

Programme basic d'application:

50 REM jean pakhomoff juillet 2021 ANGLORIN recherche de l'angle horaire du cercle horaire
passant par l'intersection d'un cadran solaire incliné avec un arc semi-diurne.
60 PI=4*ATN(1):OPEN"cadincl.docx" FOR OUTPUT AS #1
65 INPUT" latitude °, déclinaison gnomonique °, inclinaison °",FF
DGG,II
70 F=FF*PI/180:DG=DGG*PI/180:i=ii*PI/180
75 PRINT" lat = ";FF;" décl gnomo = ";DGG;" incl = ";II:PR
NT #1," lat = ";FF;" décl gnomo = ";DGG;" incl = ";II
80 J=ATN (COS (DG) /TAN (i)):JJ=J*180/PI
85 V=ATN (1/(SIN (i)*TAN (DG))):VV=V*180/PI
90 INPUT "cadran déclinant = 1; inclinant = 2: 1 ou 2?",CDS
95 IF CDS = 2 THEN 6003:rem cadi=2, kado=3
97 rem IDW IDE
100 IF J<F THEN 3000:rem cadi=1, kado=2
105 REM j>f
107 cadi=1:kado=1
145 PRINT #1,"j = ";JJ;"° v = ";VV;"°"
165 INPUT "déclinaison solaire en °?",DSS:DS=DSS*PI/180:print "déclinaison = ";DSS: print #1,"déclinaison = ";DSS
166 rem condition de validité de la déclinaison pour qu'il y ait passage sur le cadran
167 gosub 7650: if dmm=1 then 193
168 print "astre constamment sur ou sous le cadran: ni lever ni coucher."
169 print #1, "astre constamment sur ou sous le cadran: ni lever ni coucher.":end
187 rem heures de passages sur le cadran
193 gosub 7000 rem: passages dans le plan du cadran calcul de R
1400 goto 9015

3000 rem j<f j v cadi kado sont connus.
3003 cadi=1:kado=2
3055 INPUT "déclinaison solaire en °?",DSS:DS=DSS*PI/180:print "déclinaison = ";DSS: print #1,"déclinaison = ";DSS
3056 rem condition de validité de la déclinaison pour qu'il y ait passage sur le cadran
3060 gosub 7660: if dmm=1 then 3113
3065 print "astre constamment sur ou sous le cadran: ni lever ni coucher."
3070 print #1, "astre constamment sur ou sous le cadran: ni lever ni coucher.":end
3105 rem heures de passages sur le cadran
3113 gosub 7000:rem passages dans le plan du cadran calcul de R

5990 rem cadrans inclinés inclinant (face tournée vers le nord)
6003 cadi=2:kado=3
6055 INPUT "déclinaison solaire en °?",DSS:DS=DSS*PI/180:print "déclinaison = ";DSS: print #1,"déclinaison = ";DSS
6057 rem condition de validité de la déclinaison pour qu'il y ait passage sur le cadran
6060 gosub 7670: if dmm=1 then 7000

6065 print "astre constamment sur ou sous le cadran: ni lever ni coucher.":end
6070 print #1, "astre constamment sur ou sous le cadran: ni lever ni coucher.
":end
6105 rem heures de passages sur le cadran
7000 rem sous-programme: heures d'apparition et disparition de l'astre sur le plan du cadran
7010 NMUW=1/(TAN(DG)*SIN (J)):NMUW= ATN (NMUW):if NMUw<0 then NMUw=NMUW+pi
7030 REM calcul de la déclinaison dl pour laquelle R = pi/2
7035 gosub 7040:goto 9015
7040 IF KADO=1 THEN DL=SIN (NMUW)*SIN (J-F):DL=ATN (SQR(1-DL^2)/DL):PRINT "R = p
i/2 pour dl = ";DL*180/PI: PRINT #1,"R = pi/2 pour dl = ";DL*180/PI:GOTO 7050
7042 IF KADO = 2 THEN DL=SIN (NMUW)*SIN (F-J):DL=ATN (SQR(1-DL^2)/DL):PRINT "R =
pi/2 pour dl = ";DL*180/PI: PRINT #1,"R = pi/2 pour dl = ";DL*180/Pi:GOTO 7050
7045 DL=SIN (NMUW)*SIN (F+J):DL=ATN (SQR(1-DL^2)/DL)
7047 PRINT "R = pi/2 pour dl = ";DL*180/PI: PRINT #1,"R = pi/2 pour dl = ";DL*18
0/PI
7050 REM calcul de R sin R=sin NMUw sin (j-f)/cos d
7052 if kado=1 then R=SIN (NMUW)*SIN (J-F)/COS (DS):R=ATN (R/SQR(1-R^2)):goto 7070:REM sinus par l'atn
7054 if kado=2 then R=SIN (NMUW)*SIN (f-j)/COS (DS):R=ATN (R/SQR(1-R^2)):print "R = ";R:goto 7070
7060 R=SIN (NMUW)*SIN (J+F)/COS (DS):R=ATN (R/SQR(1-R^2))
7070 IF CADI=1 THEN 7145
7075 cadi = 2, cas des inclinants
7080 IF J>PI/2-F THEN 7090
7085 IF DS < DL THEN RNR=R*180/pi:GOTO 7153
7086 R = PI-R
7087 RNR=R*180/pi:GOTO 7153
7090 IF DS > DL THEN RNR=R*180/pi:GOTO 7153
7091 R = PI-R
7092 RNR=R*180/pi:GOTO 7153
7145 rem cadi =1, cas des déclinants j>f et j<f
7150 IF ABS (DS)<DL THEN RNR=R*180/pi:GOTO 7153
7151 R = PI-R
7152 RNR=R*180/pi
7153 print "R = ";RNR:print #1,"R = ";RNR
7155 IF KADO=2 THEN 7170
7160 IF KADO = 3 THEN 7175
7165 A=COS (DS):B=-TAN (J-F)*SIN (DS):C=-TAN (J-F)/TAN (R):GOTO 7190: REM kado=1
7170 A=COS (DS):B=+TAN (F-J)*SIN (DS):C=-TAN (F-J)/TAN (R):GOTO 7190
7175 A= - COS (DS):B=-TAN (J+F)*SIN (DS):C=TAN (J+F)/TAN (R)
7180 REM on prend tad pour l'angle horaire d'apparition ou de disparition et on
pose tg (tad/2)=k
7185 REM résolution ensuite de l'équation (A-B) k²+2 kC+A+B=0 2 racines R1
et R2
7190 DELTA=4*C^2-4*(A-B)*(A+B):IF DELTA>0 OR DELTA = 0 THEN 7210
7200 PRINT "delta < 0: il n'y a pas de racines, astre sur l'horizon:print #1, "
il n'y a pas de racines, astre sur l'horizon ":pdr=1:return
7210 R1=(-2*C+SQR (DELTA))/(2*(A-B))
7220 TADH=2*ATN (R1)*180/pi
7222 if TADH<0 then TADH=TADH+180
7223print "angle de passage R1 = ";tadh
7224 TADHAN=TADH
7225 TADH=TADH/15
7230 R2=(-2*C-SQR (DELTA))/(2*(A-B))
7240 TADHH=2*ATN (R2)*180/pi
7242 if TADHH<0 then TADHH=TADHH+180
7243 print "angle de passage R2 = ";tadhh
7244 TADHHAN=TADHH
7245 TADHH=TADHH/15
7250 return

7650 dm=pi/2-(j-f):if abs(ds)<dm then dmm=1:return:il y a des levers et couchers
7653 dmm=0:return:rem il n'y a pas de levers ni de couchers j>f
7660 dm=pi/2-(f-j):if abs(ds)<dm then dmm=1:return:il y a des levers et couchers
7663 dmm=0:return:rem il n'y a pas de levers ni de couchers j<f
7670 dm=abs(pi/2-(f+j)):if abs(ds)<dm then dmm=1:return:il y a des levers et couchers
7673 dmm=0:return:rem il n'y a pas de levers ni de couchers inclinants

9015 print "j = ";j*180/pi;" V = "; v*180/pi:print #1," j = ";j*180/pi;" V = "; v*180/pi
9020 print "heure d'ap ou de disp";tadh;" R1 = ";R1:print #1,"heure d'ap ou de disp tadh";tadh;" R1 = ";R1
9025 print "heure d'ap ou de disp";tadhh;" R2 = ";R2:print #1,"heure d'ap ou de disp tadhh";tadhh;" R2 = ";R2
9030 INPUT "Arrêt = a; autre angle horaire = p: a ou p, ?", a$
9040if a$ = "p" then 9060
9050 end
9060 if cadi = 1 then if kado = 1 then 160
9080if cadi = 1 then if kado = 2 then 3050
9090 goto 6003