La droite sacrée de Saint Michel Archange
Approche loxodromique
3è partie
Nous avons vu dans le paragraphe précédent que l'alignement envisagé n'existait pas sur une direction orthodromique
(chemin le plus court sur la sphère entre deux points).
Mais qu'en est-il sur un trajet loxodromique?
En othodromie l'angle de départ entre le méridien de départ et le grand cercle passant par le point de départ et le point d'arrivée
va varier constamment sur le trajet entre les deux points. Le navigateur devra faire souvent le point pour
respecter le trajet orthodromique.
En loxodromie l'angle de départ, le cap, va être invariable. Le trajet ne se fait plus alors sur un grand cercle mais
sur une spirale logarithmique.
Cette spirale va couper les méridiens traversés sous le même angle de cap et, sur une projection de Mercator on obtient
une droite sécante coupant les méridiens rendus parallèles sous un même angle entre les lieux considérés.
Cette façon de faire paraît mieux convenir aux navigateurs bien qu'elle allonge le trajet.
Voyons ci-dessous comment calculer l'angle de cap et la distance parcourue en loxodromie entre deux points du globe.
Si cet angle de cap est le même pour tous les points envisagés entre Cap Skelling et le Mont Carmel on pourra en déduire que
ces points sont alignés sur la même spirale loxodromique.

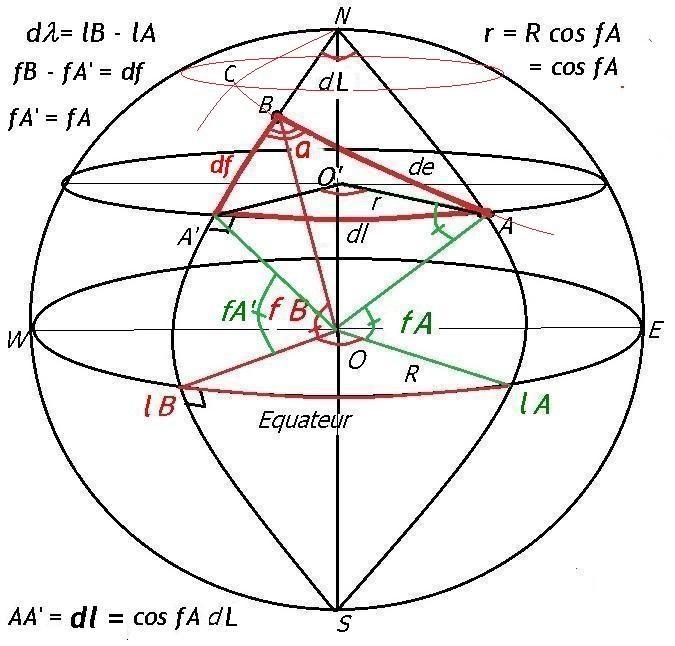
Soit donc sur le globe terrestre de rayon R=1 un lieu B de latitude fB et de longitude lB et un lieu A de latitude fA et de longitude lA.
On appelle dL la différence lB (ouest) - lA (est) des longitudes de B et A.
On se propose d'aller de B en A selon un trajet loxodromique d'angle de cap égal à a.
Le triangle BA'A est rectangle en A' car les méridiens et parallèles forment des angles droits. AA' constitue la portion de
parallèle passant par A comprise entre les méridiens passant par A et B.
BA' est la différence de latitude entre B et A. O'A = r = R cos fA = cos fA et AA' = dl = cos fA dL
L'angle de cap est a. On a tg a = dl/df et dl = tg a df
Donc cos fA dL = tg a df et df / cos fA = dL / tg a. Tous les points du trajet loxodromique répondent à ce type d'équation que
l'on pourra alors généraliser en écrivant df / cos f = dL / tg a et en intégrant cette égalité on obtient
S (1/ cos f) df = l / tg a + C ___(1)
C étant la constante d'intégration.
posons tg (f/2) = t. Alors f/2 = arc tg t et f = 2 arc tg t
La dérivée de la fonction inverse arc tg t est égale à (1/(1+t²)) dt et donc df = 2 dt /(1+t²)
Pour cos f la formule de l'arc moitié donne cos f = (1-t²) / (1+t²) et (1) peut alors s'écrire
S [(1+t²)/(1-t²)] (2 dt /(1+t²)) = 2 S [(1/(1-t²)] dt = -2 S [(1/(t²-1)] dt ___________(2)
Ecrivons l'expression 1/(t²-1) sous la forme d'une addition en introduisant 2 valeurs arbitraires x et y.
1 / (t²-1) = 1 / ((t+1)(t-1)) = x/(t+1) + y/(t-1). Réduisons au même dénominateur; le numérateur devient
x (t-1) + y (t+1) = xt-x + yt+y= t (x+y) -x + y. t n'étant pa au numérateur x+y = 0 et x = -y. Donc -x+y = 1 = 2y
d'où y = 1/2 et x+1/2 = 0 d'où x = - 1/2. On reporte alors ces valeurs dans (2)
-2 S [(1/(t²-1)] dt = -2 S (x/(t+1)) dt + y/((t-1)) dt = -2 S (-1/2 /(t+1)) dt + (1/2/(t-1)) dt = S (1/(t+1)) dt - S (1/(t-1)) dt
La primitive de 1/X étant logarithme népérien de [X] on a finalement avec t = tg (f/2) _______[ ] étant la valeur absolue
S (1/ cos f) df = ln [(t+1)] - ln [(t-1)] = ln [(t+1) / (t-1)] + C constante d'intégration.____ tg (pi/4) = 1 donc
ln [(t+1) / (t-1)] = ln [(tg (f/2) + tg (pi/4) / (tg (f/2) - tg (pi/4)] = ln [(tg (f/2) + tg (pi/4) / (tg (f/2) tg (pi/4) - 1)]
rappel: tg (a+b) = (tg a + tg b) / (1 – tg a tg b)
Donc ln [(tg (f/2) + tg (pi/4) / (tg (f/2) tg (pi/4) - 1)] = ln [ - tg (f/2 + pi/4)]
et S (1/ cos f) df = ln [ - tg (f/2 + pi/4)] + C _____(3)
Le lieu A correspondra à ln [ - tg (fA/2 + pi/4)] + C = lA / tg a + C _________(4)
Le lieu B correspondra à ln [ - tg (fB/2 + pi/4)] + C = lB / tg a + C__________(5)
En soustrayant (4) à (5) on obtient
ln [ - tg (fB/2 + pi/4)] + C - (ln [ - tg (fA/2 + pi/4)] + C) = lB / tg a + C - (lA / tg a + C) = (lB - lA) / tg a
et
tg a = (lB - lA) / ln [ - tg (fB/2 + pi/4)] - (ln [ - tg (fA/2 + pi/4)]
La distance loxodromique de entre les lieux A et B correspond à de cos a = BA' et de = BA' / cos a ce qui correspond au
chemin loxodromique BA = BA' R / cos a = (fB - fA) R / cos a
R étant le rayon terrestre.
Utilisant ces résultats j'ai calculé le cap (angle de départ à partir de l'ouest) pour quelques uns de ces lieux eu utilisant leurs coordonnées
géographiques exposées dans la partie précédente.
Voici les résultats obtenus:
Cap Skelling-Mont Saint Michel: 89.43511°
Cap Mont Saint Michel-Abbaye Saint Michel de la Cluse dans le Piémont: 89.41509°
Cap Skelling- Abbaye Saint Michel de la Cluse dans le Piémont: 89.42506°
Cap Skelling-Carmel: 89.42568°
Cap Skelling-Angkor: 89.58625°
Ces valeurs étant très proches les unes des autres on peut donc conclure que ces différents lieux
sont alignés sur une spirale loxodromique.
Jean Pakhomoff
24 10 2020
http://serge.mehl.free.fr/anx/loxodromie.html
http://exo7.emath.fr/ficpdf/fic00108.pdf
Retour à "mes travaux en gnomonique"