Etude de la connaissance de l'heure et de la date
par la mesure de la direction et de la hauteur du
soleil sur un horizon de latitude donnée
suivie
de l'étude théorique d'un
cadran solaire
tracé sur le périmètre d'une calotte sphérique
Jean Pakhomoff
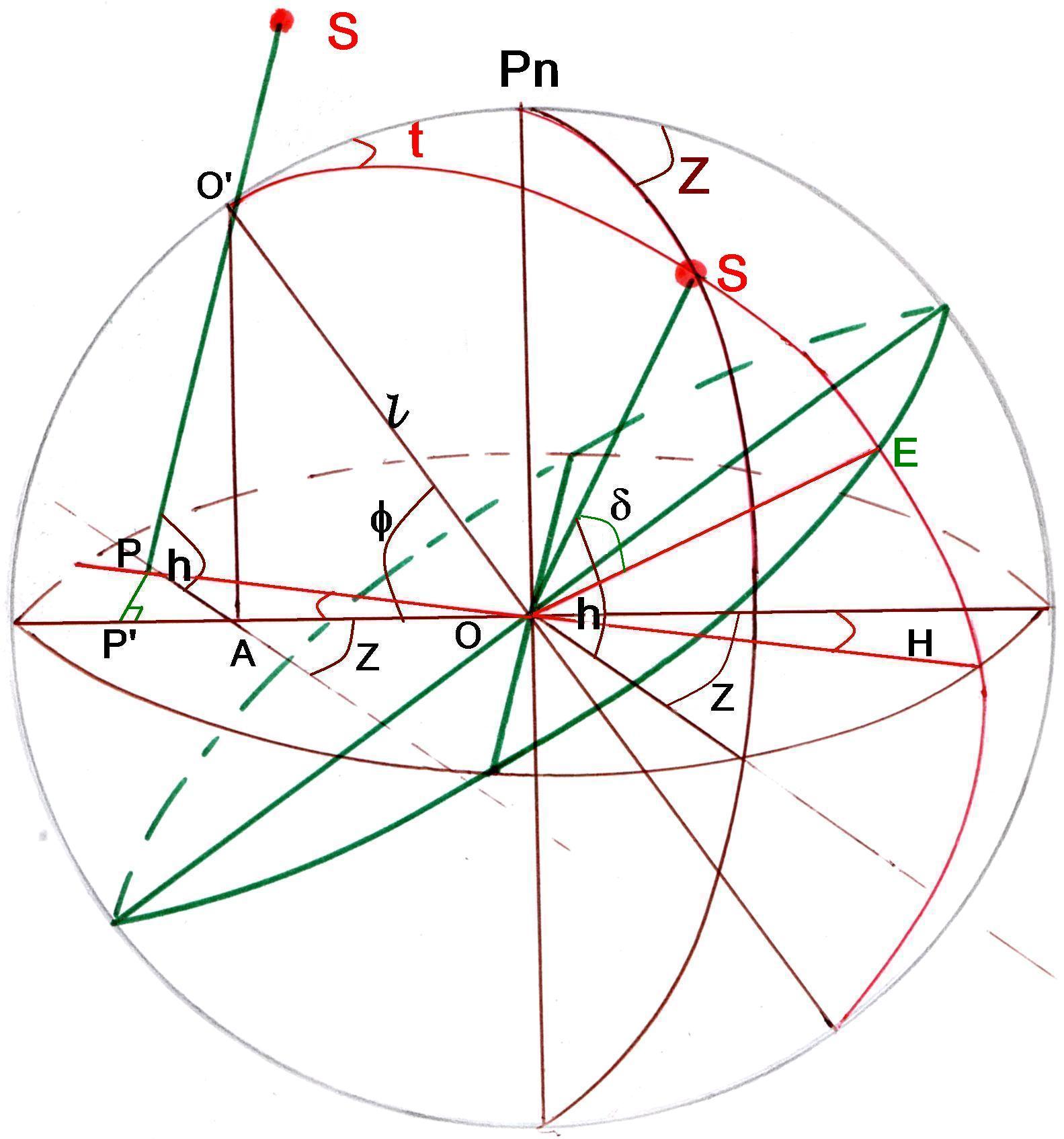
Soit donc une sphère céleste de centre O avec le soleil S sur un horizon de latitude f.
Par S passe le cercle horaire O's correspondant à l'angle horaire t donnant avec l'horizon l'angle H.
Par S passe aussi le vertical PnS donnant avec l'horizon l'angle d'azimut Z.
Le cercle horaire donne avec l'équateur l'angle SOE égal à d la déclinaison du moment.
Par un point O' de l'axe polaire abaissons une perpendiculaire en A sur la méridienne de façon à obtenir
le cadran horizontal O'AO de style OO' égal à l.
Le vertical passant par 0'A coupe la ligne horaire en P. Le rayon solaire de hauteur h passant par O' vient en P
puisque un rayon est la trace de l'intersection du cercle horaire avec le vertical de l'astre.
Projetons P sur la méridienne en P'.
On peut alors écrire que O'A / AP = tg h , AP= l sin f / tg h , AP' = AP cos Z = l sin f cos z / tg h
PP' = AP sin Z = l sin f sin Z / tg h , OP' = OA + AP' = l cos f + l sin f cos Z / tg h
PP' / OP' = tg H PP' = OP' tg H d'où
l sin f sin Z / tg h = l cos f tg H + l sin f cos Z tg H / tg h et en divisant cette égalité par l sin f et
en la multipliant par tg h on obtient sin Z = tg H tg h / tg f+ cos Z tg H
En remplaçant tg H par sa valeur connue tg t sin f on obtient après simplifications:
tg t = sin Z / (tg h cos f + cos Z sin f)
Ce qui permet d'avoir l'heure à partir de l'azimut, de la latitude et de la hauteur.
Connaissant t passons alors au triangle paralactique PnO'S où PnS = p / 2 - h , O'S = p / 2 - d
et PnO' = p / 2 -f , PnO's = t et O'PnS = p-Z
on a donc sin t / sin PnS = sin ( p - Z) / sin (p/2 - d) ou sin t / cos h = sin Z / cos d
et cos d = sin Z cos h / sin t
ce qui permet de connaître la date (choisir entre deux dates possibles)

Le 30 août 2011
***************************
Théorie d'un cadran solaire
tracé sur le périmètre
d'une calotte sphérique
Cela revient à trouver les coordonnées horizontales de l'intersection du vertical et du cercle horaire choisi sur le cercle sommet de la calotte.
Nous aurons à nous servir dans ce travail de la formule
tg t = sin Z / (tg h cos f + cos Z sin f) (1)
que nous avons établie ci-dessus où t est l'angle horaire choisi, h la hauteur de l'intersection
du cercle horaire et du vertical, Z l'azimut de celle-ci et f la latitude.
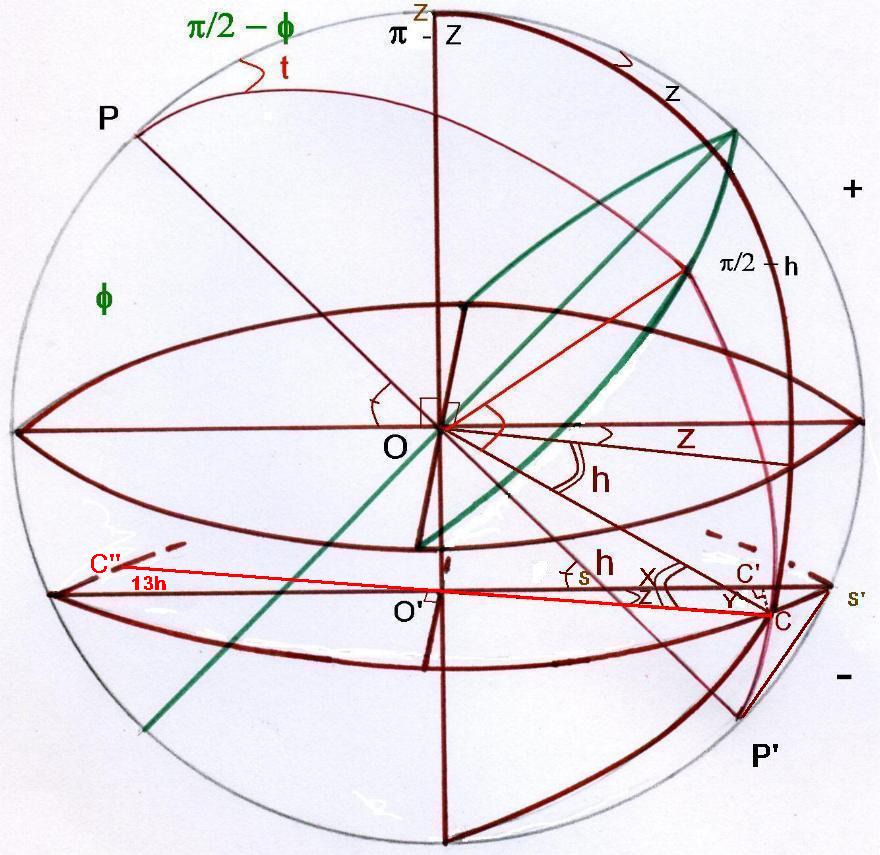
Soit donc une sphère céleste de centre O, d'axe polaire OP. Soit un horizon O de latitude f .
Un cercle horaire PC correspondant à l'angle horaire t coupe le vertical ZC en C sur la calotte
dont le plan horizontal est O'C'C . Cette calotte est arbitrairement choisie de façon à ce que OO' = z
On aura z / O'C = tg h où h sera la hauteur sur la sphère du point C.
Dans notre cas de figure le point C étant sous l'horizon la hauteur doit être comptée négativement.
Ainsi dans le triangle paralactique PZC on a ZC = p / 2 - h (avec h < 0)
Donc O'C = z / tg OCO' = z / tg (p / 2 - h - p / 2) = z /( - h)
Le problème essentiel est de trouver l'azimut Z.
A partir de la formule (1) nous pouvons écrire
tg t tg h cos f + tg t cos Z sin f = sin Z
en élevant au carré les deux membres de cette équation et après développement il vient
cos² Z (tg² t sin² f + 1) + cos Z (2 tg² t tg h sin f cos f ) + tg² t tg² h cos² f - 1 = 0
X²a + Xb +C = 0
ce qui est une équation du second degré donnant deux racines dont l'une répond à la question.
Exemple chiffré :
h = - 30°, f = 43°, t = 15° (1 heure de l'après-midi)
on trouve alors a = 1.03339424 b = - 0.0413509 et C = - 0.9871991 ce qui nous donne
Z = 4.2918° et Z = 163.25° La valeur à retenir est 4.2918 car sous l'horizon l'angle d'azimut devient plus petit que l'angle horaire.
En projetant c sur O'C' il vient O'C' = O'C cos Z = z cos Z / tg h = X
CC' = O'C sin Z = z sin Z / tg h = Y
Si on choisit un rayon de la sphère origine égal à 0.5 m avec les paramètres ci-dessus on obtient
z = OC sin h = 0.5 sin - 30 = - 0.25 O'C = z / tg (h) = - 0.25 / -0.57735 = 0.433 m
O'C' = X = 0,4317 m et CC' = Y = 0.0324 m
On refera ces calculs pour chaque heure de façon à positionner les '' points d'heure ''.
Il faudra en outre prendre le point C'' symétrique de C sur la calotte sphérique par rapport à O
pour obtenir le point de 13 h correspondant à l'angle horaire t = 15° et on opérera de la même façon pour tous les autres angles horaires.
De même par symétrie et sans autres calculs on obtiendra les heures du matin.
Par le point S situé sur O'S' sortira le style faisant un angle f avec l'horizontale dans le plan méridien.
On pourra pour cela construire un triangle gabarit SS'P'.
On aura SP' = PP' - OS = 2 R - (R + z/ sin f ) = R + z / sin f
SS' = O'S' - O'S = O'C - O'S = z / tg h - z / sin f
P'S'² = SP'² + SS'² - 2 SP' SS' cos f d'où P'S'
Une fois ce triangle convenablement positionné dans le plan méridien on fera glisser sur le côté SP' l'axe polaire.
Les cadrans solaires de Jean Pakhomoff
6 9 2011
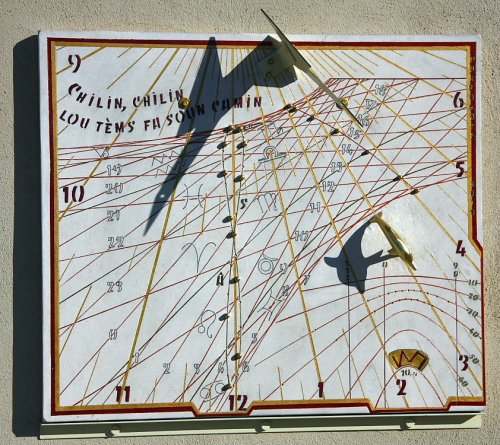
Cadran solaire montrant les
heures solaires
heures italiques
heures babyloniques
heures sidérales
équation du temps
arcs diurnes zodiacaux
moment de la prière du Asr
Le dauphin par l'ombre de son rostre montre
les hauteurs et azimuts du soleil