Etude du style d'un cadran à polo
Précisions sur la sous-stylaire et l'équinoxiale
Nous avons vu dans le paragraphe consacré aux cadrans bifilaires comment tracer sur un cadran classique à polo les lignes d'heures, arcs diurnes et autres objets gnomoniques.
Nous allons étudier ici le style d'un tel cadran à savoir le gnomon qui par son ombre permettra d'utiliser les lignes horaires et les diverses courbes du cadran.
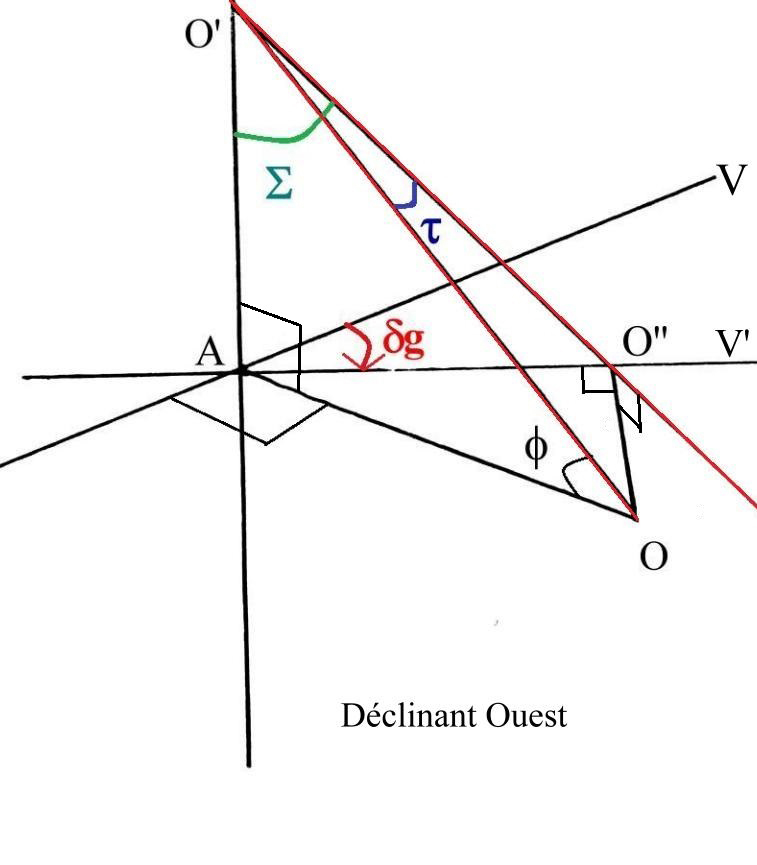
Soit donc un tel style OO' de longueur OO' = l que l'on situe dans le plan méridien sur l'axe de rotation de la terre faisant un angle f avec l'horizontale OA obtenue en projetant
O sur le cadran dans ce plan méridien.
L'ombre de OO' marquera les heures et le rayon de soleil passant par le point O donnera les indications de dates, d'heures italiques, hauteurs, azimuts etc…

fig 1
Ce style perce le cadran O'AV' en O'. Ce cadran a décliné de dg par rapport au cadran méridional correspondant O'AV dont le plan est situé dans le premier vertical.
Nous avons choisi le cas de figure d'un déclinant Ouest mais les équations sont identiques pour le déclinant Est ou pour les inclinants (orientés au nord) Est et Ouest.
Le style principal OAO' n'est pas utilisé en dehors des cadrans plein sud. En effet lorsque le mur décline ce qui est le cas habituel, sa pose s'avère très délicate.
On préfère se servir du style secondaire OO'O'' qui permet par son implantation perpendiculaire au plan du cadran une pose bien plus simple.
Faisons passer par A une horizontale tracée sur le cadran.
Projetons orthogonalement le point O en O'' sur cette horizontale. Ce point O'' se situe sur une ligne horaire particulière qui est appelée sous-stylaire du cadran.
Nous donnerons plus loin quelques indications sur cette dernière.
On peut donc écrire OO' = l O'A = l sin f et OA = l cos f
AO'' = OA cos (p/2 – dg) = OA sin dg = l cos f sin dg
OO" = OA sin (p/2 – dg) = l cos f cos dg
O'O''O rectangle en O'' nous permet d'écrire O'O'' ² + OO'' ² = OO' ² =
l ² + l ² cos f ² cos dg ²
O'O'' ² = OO' ² - OO'' ² = l ² - l ² cos f ² cos dg ²
et O'O'' = l v ¯(1 - cos f ² cos dg ²)
En appelant t l'angle OO'O" fait par le style et la sous-stylaire on a
OO" = l sin t ==> sin t = OO" / l = cos f cos dg
La connaissance de la valeur de cet angle t est d'une grande importance dans la construction du style secondaire du cadran solaire ou du gabarit sur lequel on fera glisser le style principal.
En appelant S l'angle AO'O" fait par la sous-stylaire et la méridienne O'A
on a tg S= AO" / O'A = l cos f sin dg / l sin f = sin dg / tg f et tg S = sin dg / tg f
Nous retrouverons cet angle plus bas lorsque nous traiterons de l'équinoxiale.
Nous avons ainsi tous les éléments nécessaires à la construction d'un style de cadran solaire.
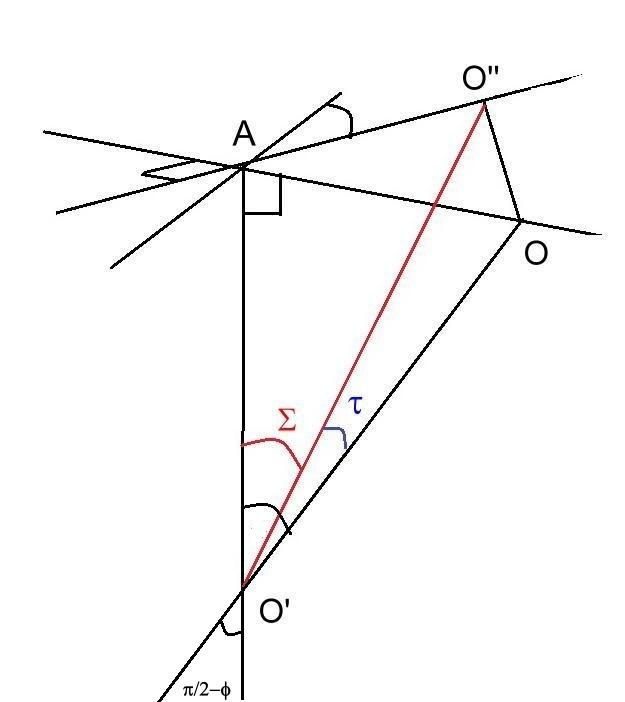
fig 2
Cas de figure d'un inclinant Nord-Est
Equinoxiale et sous-stylaire
Les arcs diurnes se trouvent représentés sur les cadrans solaires par des courbes, hyperboles, paraboles ou ellipses selon la latitude.
Sous nos latitudes inter arctiques ce sont des hyperboles (voir la théorie des coniques pour complément d'information).
Seule la "courbe" correspondant aux équinoxes est une droite qui se confond sur le cadran avec la trace de l'intersection du plan de l'équateur céleste avec le plan du cadran.
Cette droite décrite par l'ombre d'un point choisi du style rend compte de la course du soleil sur l'horizon lorsqu'il se trouve dans l'équateur céleste sa déclinaison étant alors nulle.
Les cercles horaires espacés de 15 en 15° sur la sphère céleste ont tous pour axe l'axe des pôles et sont tous perpendiculaires à l'équateur céleste.
Selon la déclinaison du cadran on verra cette équinoxiale plus ou moins penchée sur l'horizon. C'est ce que l'on peut constater sur les cadrans ci-dessous:
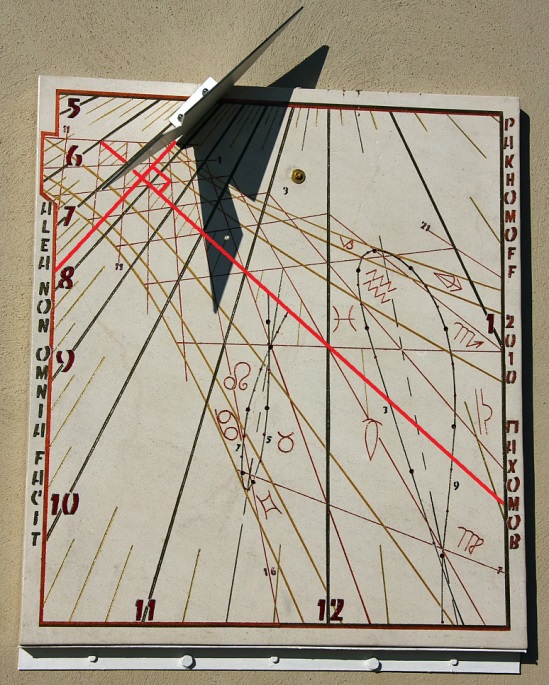

A gauche un déclinant fortement à l'Est. On constate que l'équinoxiale est perpendiculaire à la sous-stylaire qui se situe environ sur 7h 45 solaire.
A droite un déclinant faiblement à l'Ouest. Là l'équinoxiale est proche de l'horizontale et elle fait un angle perpendiculaire avec la ligne horaire proche de
14h 15 civile heure d'été ce qui correspond ici à environ 12h 25 solaire.
Tentons de donner une explication géométrique à ces différentes positions de l'équinoxiale sur les cadrans puis recherchons quelle est la valeur de l'angle d'inclinaison p
de l'équinoxiale sur l'horizon et enfin comparons cette valeur à celle de l'angle S compris entre la méridienne et la sous-stylaire.
Pour cela observons la figure 3
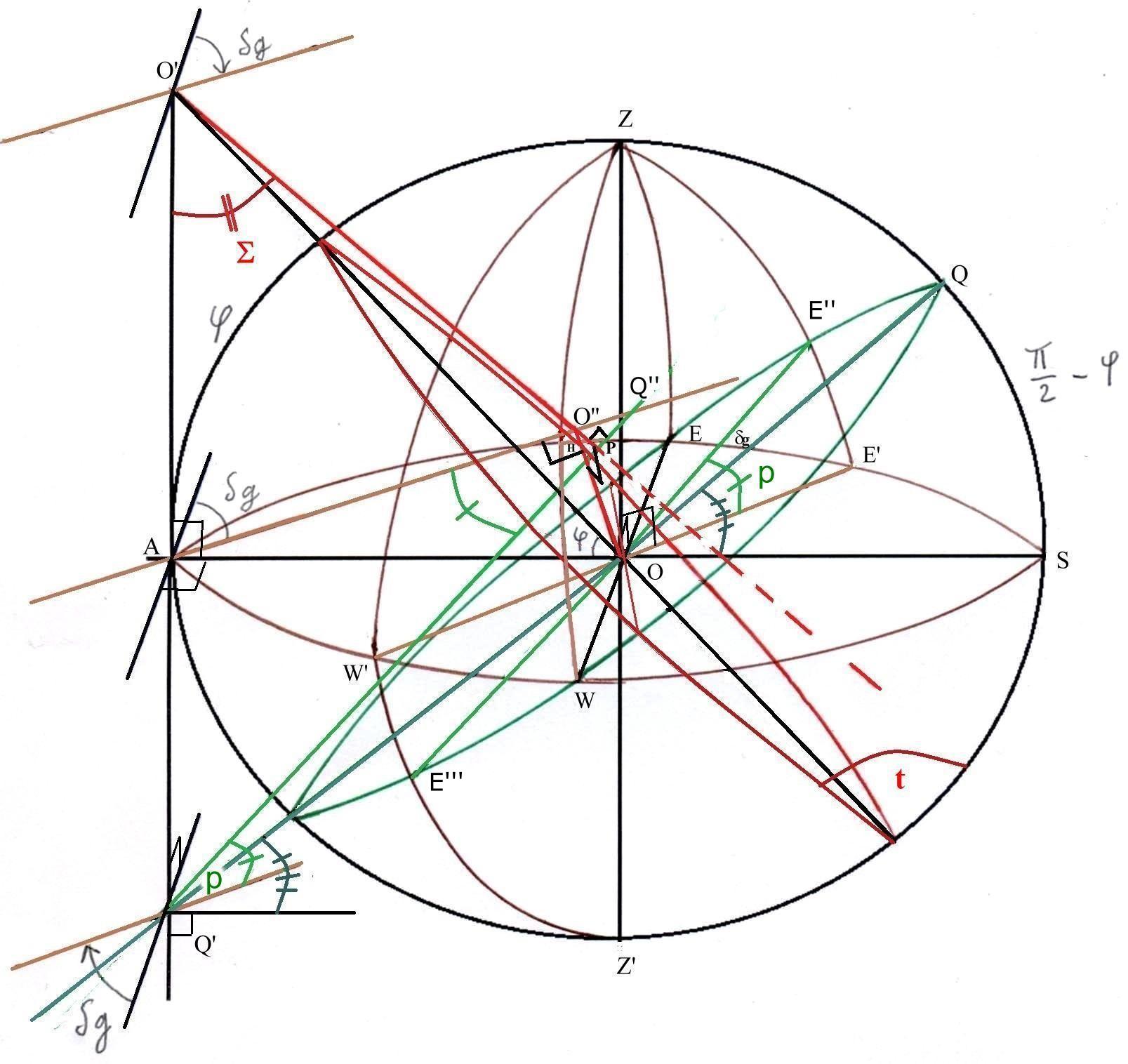
fig 3
On a figuré au bout de notre style OO' une sphère céleste de centre O. L'axe de rotation de la terre OO' va pénétrer le mur sur lequel est installé notre cadran en O'.
On a représenté le grand cercle de l'équateur céleste EQW en vert. Il est perpendiculaire en O à l'axe des pôles. Nous traçons le premier vertical WZE.
Le grand cercle de l'horizon AESW, le grand cercle de l'équateur et le premier vertical ont leur intersection sur la droite WE direction Ouest Est perpendiculaire à l'axe nord sud.
Faisons pivoter le premiet vertical d'un angle dg égal à la déclinaison gnomonique de façon à ce que E vienne en E' et W en W'. Nous obtenons le vertical parallèle au plan de notre cadran.
Ce vertical coupe l'équateur céleste en E'' et E''' donnant la droite de coupe E''E'''. C'est l'équinoxiale de notre cadran. En effet le plan de l'équateur vient percer le mur du cadran
selon le même angle qu'avec le vertical W'ZE' puisque ce vertical a été choisi parallèle au mur. Donc l'équinoxiale E''E''' donne son image parallèle Q'Q'' sur le mur.
Notre cas de figure étant un déclinant ouest par Q'' passera la ligne tabulaire horaire de 18 h solaire puisque Q'' est l'intersection de l'horizon avec l'équinoxiale (6h solaire si le cadran décline à l'Est).
Nous avons vu plus haut que la sous-stylaire O'O'' était obtenue par la projection d'un point O du style sur le plan du cadran. Le plan OO'O'' obtenu en agissant ainsi correspond
au cercle horaire d'angle horaire t perpendiculaire au plan du cadran. Ce cercle étant perpendiculaire au plan du cadran l'est aussi, comme tous les autres cercles horaires,
au plan de l'équateur céleste et leurs traces sur le cadran sont donc des droites perpendiculaires en P.
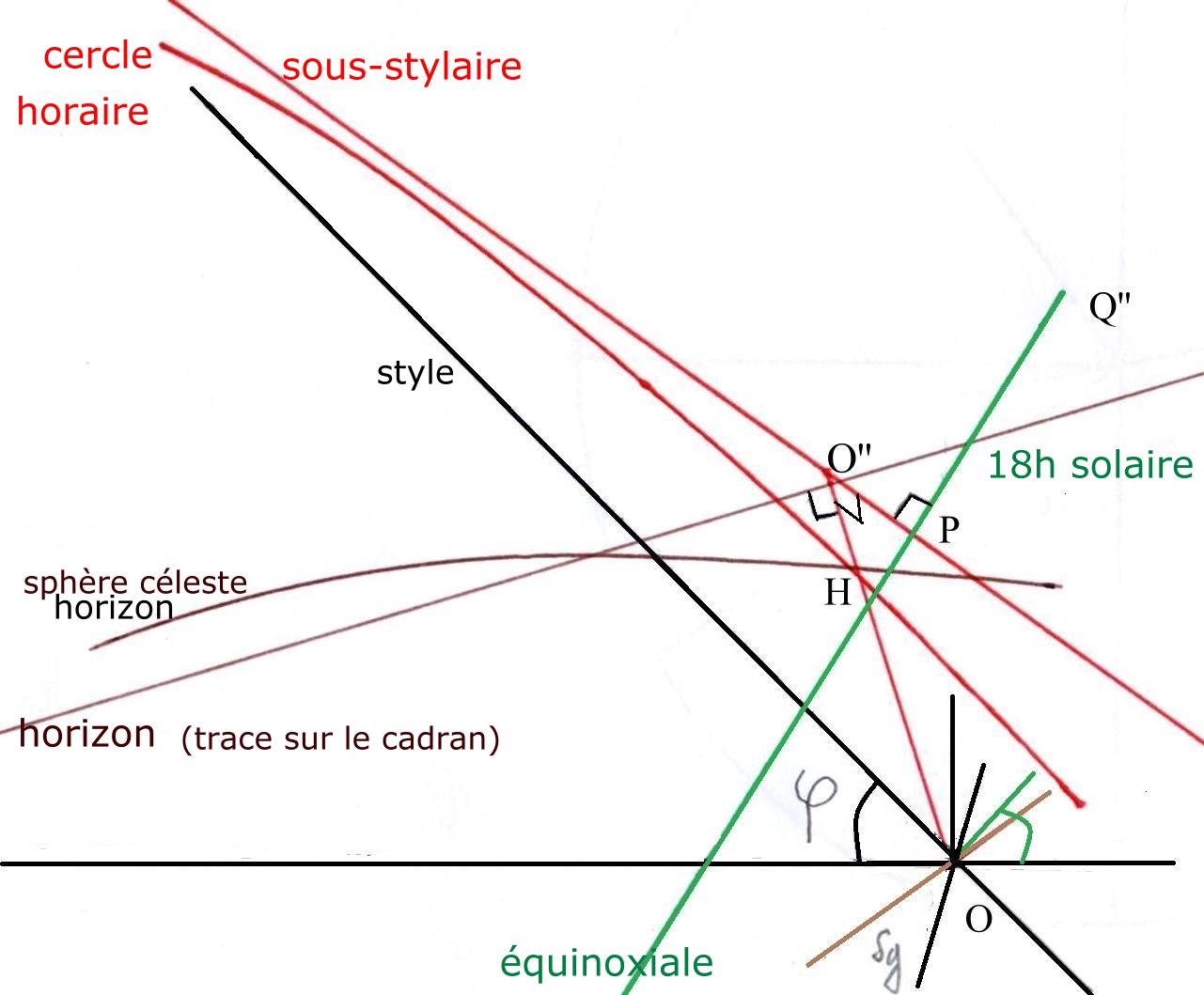
fig 3' _ détails de la figure 3
Sur les cadrans solaires l'équinoxiale et la sous-stylaire sont perpendiculaires.
Cherchons quelle est la valeur de l'angle E''OE' = p qui est la hauteur de l'équinoxiale sur l'horizon après rotation du vertical. Par simple parallélisme on retrouve l'angle E''OE'
du vertical W'ZE' en p sur le mur parallèle.
L'angle O'Q'P est égal alors à p - (p/2 +p) = p/2 - p. Le triangle O'Q'P étant rectangle en P (intersection sous-stylaire équinoxiale)
on a p/2 - p + S = p/2 et p = p/2 + S – p/2 donc
p = S
L'angle fait entre la sous-stylaire et la méridienne est égal à l'angle fait entre l'horizontale et l'équinoxiale. On a vu au début de ce travail que
tg S = sin dg / tg f Vérifions la valeur de p par le calcul direct:
Pour cela examinons la figure 4.
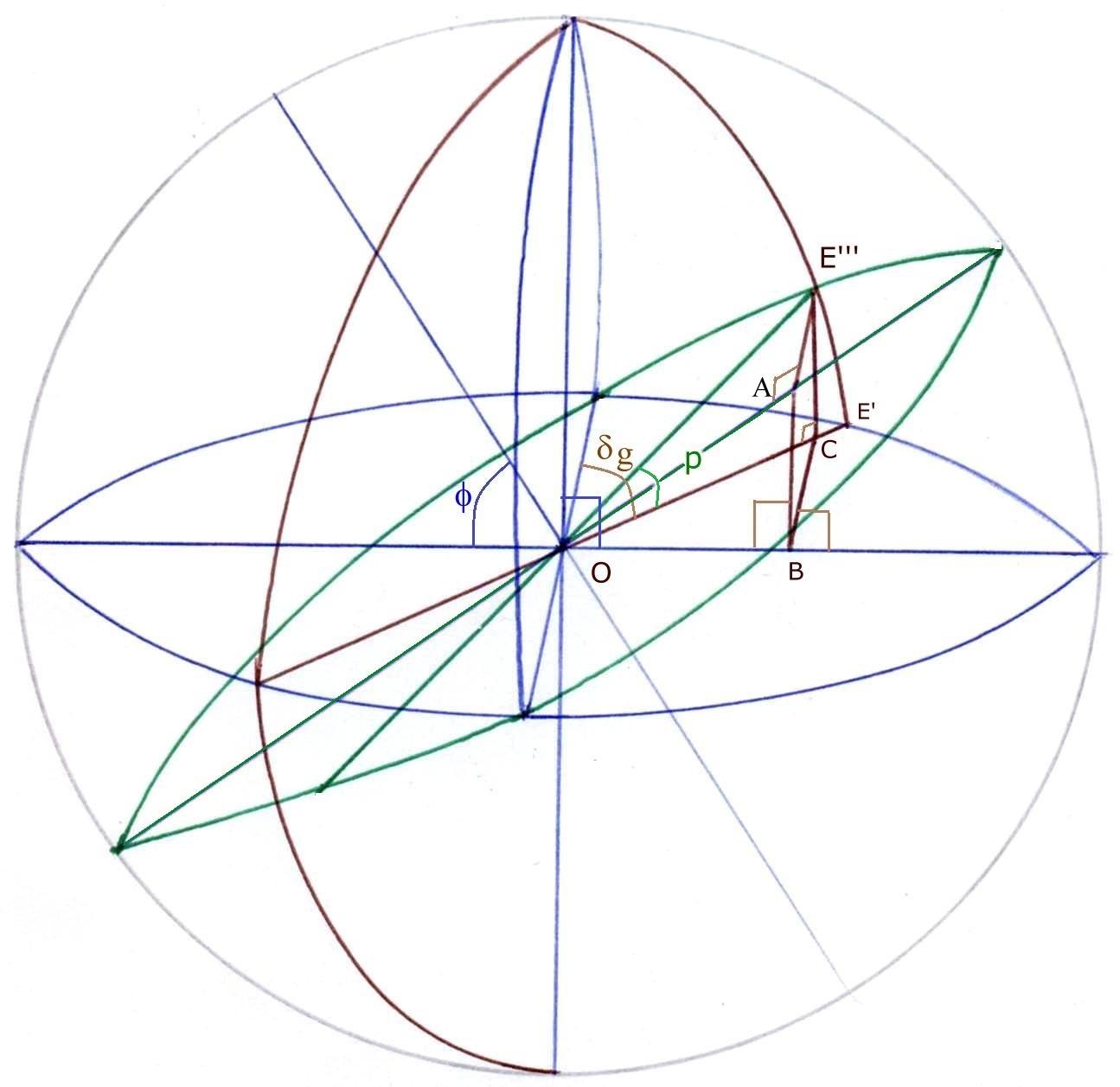
fig 4
Nous retrouvons le vertical W'ZE' qui a pivoté de dg par rapport au premier vertical WZE. W'ZE' coupe l'équateur céleste en E'''.
Imaginons un plan vertical passant par E''' et perpendiculaire aussi au plan méridien. Ce plan va donner naissance au rectangle E'''ABC.
Du triangle E'''OC on tire tg p = E'''C / OC
Du triangle OAB on tire tg (p/2 - f) = AB / OB
Du triangle OBC on tire OB = OC cos (p/2 – dg) = OC sin dg
et tg p / tg (p/2 – f) = (E'''C / OC) / (AB / OB)
ou tg p tg f = E'''C OB / OC AB AB = E'''C d'où
tg p tg f = OB / OC = OC sin dg / OC = sin dg
et tg p = sin dg / tg f = tg S
On a donc là confirmation que l'angle fait entre la sous-stylaire et la méridienne est égal à l'angle fait entre l'horizontale et l'équinoxiale.
Style du cadran horizontal
Ce style correspond à l'axe du monde incliné sur l'horizon d'un angle égal à la latitude du lieu dans le plan méridien. En prenant OO' = l
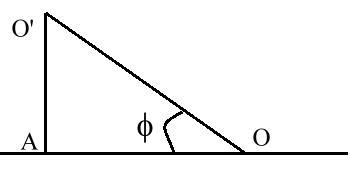
On aura O'A = l sin f et OA = l cos f
Jean Pakhomoff ___5 4 2014
Retour à Mes Travaux en Gnomonique