Les lunules d'Hippocrate de Chios
(vers -500 av JC)
et leur tangente commune
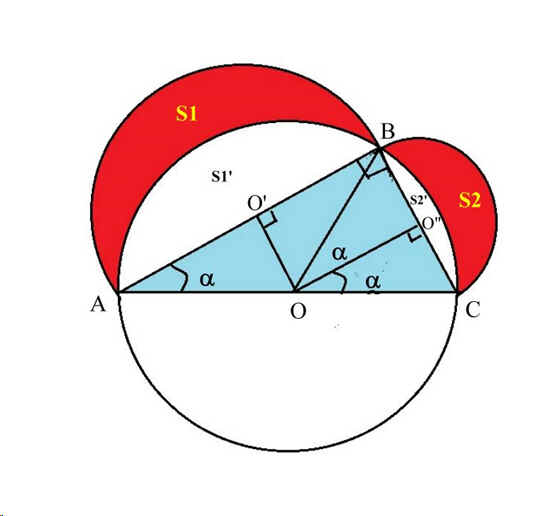
Soit un triangle ABC rectangle en B inscrit dans un cercle de centre O.
Nous choisissons arbitrairement l'angle BAC égal à a.

Traçons sur AB le demi cercle de diamètre AB et sur BC le demi cercle de diamètre BC.
Les intersections de ces cercles avec le cercle de diamètre AC = 2r déterminent les lunules S1 et S2.
Surface du ½ cercle de diamètre AB = p /8 * AB²
Surface du ½ cercle de diamètre BC = p /8 * BC²
La somme de ces deux surfaces = p /8 (AB²+BC²) = p /8 AC² d'après le théorème de Pythagore <=> surface du demi cercle de centre O.
La surface du demi cercle de diamètre AB est égale à S1 + S'1 la surface du demi cercle de diamètre AC est égale à S2 + S'2 et la surface du demi cecle de diamètre AC est égale à la surface du triangle ABC + S'1 + S'2
d'où ½ cercle AB = S1 + S'1
½ cercle AC = S2 + S'2
½ cercle AC = Surface ABC + S'1 + S'2
Nous venons de voir que ½ cercle AC = ½ cercle AB + ½ cercle AC
d'où Surface ABC + S'1 + S'2 = S1 + S'1 + S2 + S'2
et Surface ABC = S1 + S2 ce qui est le théorème d'Hippocrate de Chios (-500 av JC)
Démonstration trigonométrique:
Surface S du secteur AOB = (p -2a) / 2 p * p AO² = (p -2a) / 2 * r²
OO'=r sin a __A O' = r cos a __S AOO' = OO' AO' / 2 = r² sin a cos a /2 et S AOB = 2 S AOO' = r² sin a cos a
D'où S'1 = S secteur AOB - S AOB = (p - 2 a) / 2 * r² - r² sin a cos a et S1 = p /8 * AB² - S'1 = p /8 * AB² - (p -2 a)/2 * r² + r² sin a cos a
Le demi cercle de diamètre BC nous permet d'écrire
S2 + S'2 = p /8 * BC² __Secteur BOC = (2 a / 2 p) * p OC² = a * r²
S triangle BOC = (2* OO" * O"C / 2) = OO" * O"C = r cos a * r sin a
S'2 = a r² - r² cos a sin a et S2 = (p /8) * BC² - a r² + r² cos a sin a
S1 + S2 = (p /8) AB² - (p -2 a)/2) * r² + r² sin a cos a
_______+( p /8) BC² - a r² + r² cos a sin a =
(p /8) AC² - r² (((p -2 a)/2) + a) + 2 r² cos a sin a =
(p /8) AC² - r²( p /2 - 2cos a sin a)__ comme AC = 2 r
S1 + S2 = p r²/2 - p r²/2 + 2 r² cos a sin a
La surface des deux lunules est donc égale à 2 r² cos a sin a ce qui est également la surface du triangle rectangle AB*BC/2
Si a = 0 S1+S2 = 0 si a = p/4 (45° triangle isocèle) alors S1+S2 = r² si a = p/2 (tangence) S1+S2 = 0
Tangente commune aux lunules.
Chaque lunule possède une quantité infinie de tangentes.
Sur la figure 2 nous montrons une tangente en M sur le rayon O'M du demi cercle de centre O'. Cette tangente coupe la droite prolongeant le diamètre AC = 2 r du cercle O en K'.
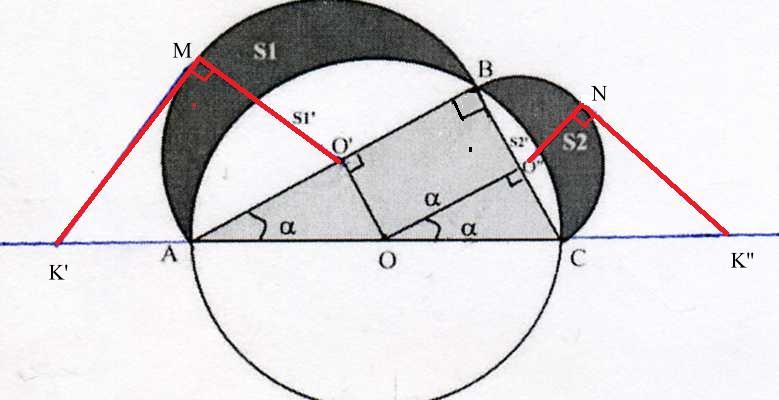 Fig 2
Fig 2
De même la tangente en N sur le rayon O''N du demi cercle de centre O'' coupe la droite prolongeant le diamètre AC du cercle O en K''.
Nous allons examiner le cas où les tangentes aux deux lunules sont confondues sur une même ligne droite MN coupant la droite prolongeant le diamètre AC du cercle O en K. (Fig 3)
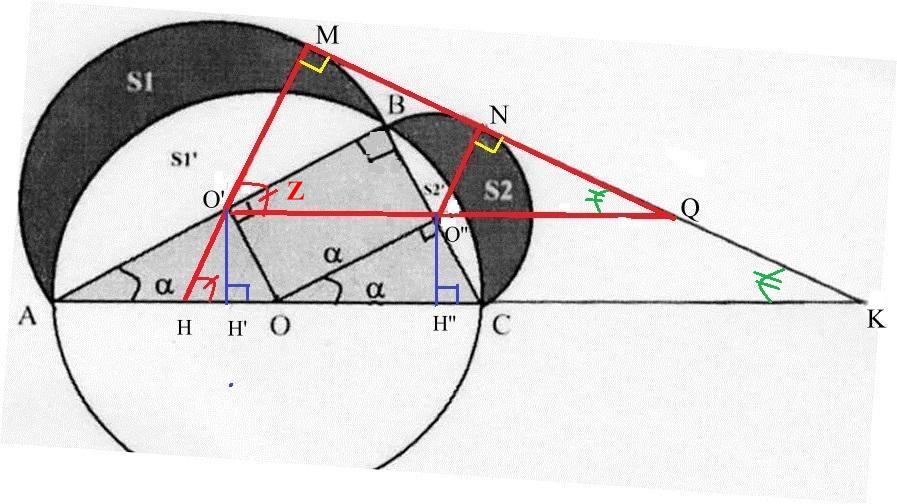 Fig 3
Fig 3
Nous obtenons le point Q en prolongeant la droite O'O'' jusqu'à son intersection avec MK.
O'O'' est parallèle à la droite AC car O'H' = r cos a sin a = O''H'' et par conséquent O'Q // AK.
Les triangles O'MQ et O''NQ sont semblables car rectangles avec l'angle MQO' commun. On peut donc écrrire les rapports:
QN/QM = QO''/QO' = NO''/MO' MO' = AO' = r cos a et NO'' = O''C = r sin a
D'où NO''/MO' = tg a = QO''/QO' = QO''/(QO''+O'O'')
Le triangle rectangle O'B0'' permet d'écrire O'O''² = O'B²+O''B² = r²cos² a + r²sin² a = r² et O'O'' = r
D'où tg a = QO''/(QO''+r) et QO'' = r tg a / (1-tg a)
QO' = QO''+O'O'' et dans le triangle rectangle O'MQ on a QO' cos Z = OM' Z étant l'angle MO'Q
d'où cos Z = OM'/QO' = r cos a / (r tg a /((1-tg a) + r)) = cos a – sin a d'où l'arc cosinus de Z
MO'Q = Z = MHK MH étant le prolongement de MO' sur AC d'où l'on tire du triangle rectangle O'H'H
O'H sin Z = O'H' = r cos a sin a et MH = MO' + O'H = r cos a + r cos a sin a = r cos a (1 + sin a)
Dans le triangle rectangle MHK on a HK cos Z = MH et HK = MH / cos Z
Dans le triangle HO'O on a O'OH = p / 2 – a ; O'HO = Z ; HO'O = p – (Z + p /2 – a) = p / 2 + a – Z
HO / sin (p / 2 + a – Z) = OO' / sin Z = r sin a / sin Z et HO = r sin a cos (a – Z) / sin Z
et OK = HK – OH
Donc la tangente commune aux deux lunules coupe le diamètre AC du cercle de centre O à la distance OK de O.
Nous remarquons que si a = 0 alors cos Z = cos a – sin a = 1 et Z = 0 : les lunules n'existent pas. Le sommet B est en C. La tangente
correspondante est celle en C au diamètre AC du cercle O.
Si a = p /4 alors cos Z = 0 et Z = p /2. C'est le cas où ABC est isocèle et la tangente commune est parallèle au diamètre AC.
si a = p /2 alors cos Z = - 1 et Z = p. Les lunules n'existent plus. Le sommet B est arrivé en A. La tangente correspondante est celle en A
au diamètre AC du cercle O.
Les points O' et O'' parcourent un demi cercle de diamètre OA pour O' et CO pour O'' quand a varie de 0 à p / 2. Si A est le centre du
repère orthonormé dont l'axe des x est AC alors x et y sont les coordonnées polaires des extrêmités O' et O'' des diamètres OA et CO
parcourant les demi cercles correpondants.
O' (x = r cos² a, y = r cos a sin a) O'' (x = 2r-r sin² a, y=r sin a cos a)
Jean Pakhomoff les 15 et 24 2 2014