Considérations sur le tracé et la
lecture d'un cadran à
heures sidérales
par
Jean Pakhomoff
gnomoniste à Marseille
1- Tracé du cadran
On se servira pour cela de points communs et de points remarquables.
a) tracé par les points communs.
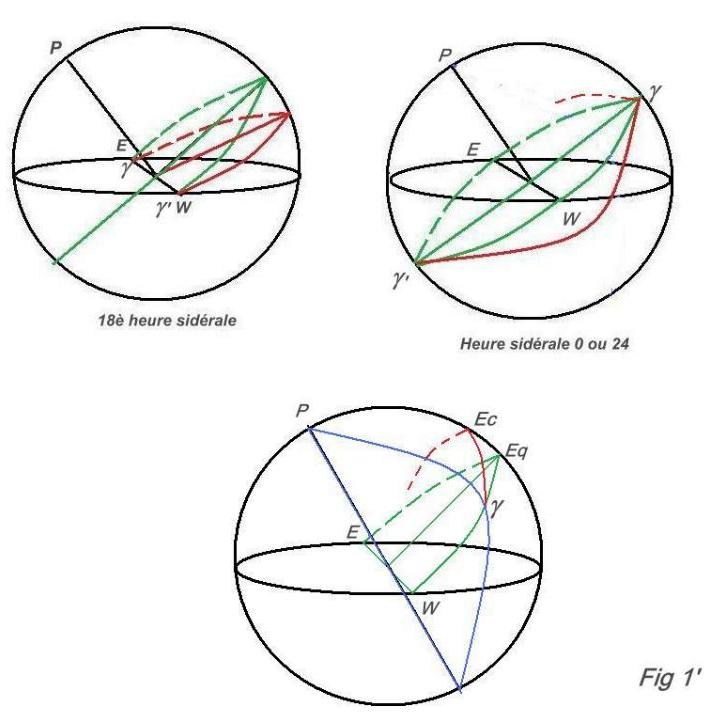
Prenons le cas de la figure 1 qui représente la sphère céleste de pôle P à 18 heure sidérale. L'écliptique est en rouge et l'équateur céleste en vert.
L'horizon NS en noir. g se lève à l'horizon Est, g ' se couche à l'Ouest, le début du Capricorne passe en C au méridien et le début du Cancer passe en K à l'anté-méridien.
fig 1
A 18 heure sidérale l'angle horaire de g sur l'équateur est de 270° et celui du début du Capricorne 0°. Il nous faudra rechercher l'angle horaire de chaque point de début de signe zodiacal pour l'heure sidérale envisagée. On se servira pour cela de la formule classique sin d = sin e sin l (1) où d est la déclinaison, e la valeur d'epsilon et l la longitude écliptique du point envisagé. Connaissant d on tire l'ascension droite a en se servant de la relation cos a = cos l / cos d (2). On affine le résultat en donnant à epsilon une valeur approchée de la réalité en considérant sa variation perpétuelle, bien que faible, dûe à différents mouvements de la planète. On se sert de la relation e = ep - k où ep (3) est la valeur d'epsilon au 1/1/1900 (23°27'8.26'') et k = 0.46845'' t (t étant le nombre d'années écoulées depuis le 1/1/1900).
Une fois a connu on tire l'angle horaire h par soustraction de a au temps sidéral envisagé. La connaissance de cet angle horaire et de la déclinaison nous permet alors de calculer les coordonnées x et y de l'intersection du rayon provenant de ce point de l'écliptique et passant par un point de notre style avec le plan du cadran.
2 points quelconques de l'écliptique fixé à une heure sidérale déterminée permettront alors en joignant leur image sur le cadran de donner la ligne de coupe du plan de l'écliptique avec le plan du cadran. Cette ligne sera l'image de notre heure sidérale.
Ainsi, en appliquant (3) au mois de Janvier 2004 on trouve e = 23.43876° (23°26'19'').
On commence par le calcul de l'angle horaire de chaque début de signe zodiacal à 18 h sidérale. Il ne nous reste plus qu'à ajouter 15° à chacun de ces résultats quand on passe à l'heure sidérale suivante.
Ainsi pour le Capricorne à 18 h sidérale on a vu que h = 0°. A 19 h sidérale h = 15°, à 20 h sidérale h = 30° etc...
Pour e = 23.43876 (janvier 2004) on trouve pour le Verseau (l = 300°) à 18 h sidérale a = 302.18115° et h = 327.8188° (32.1812° anté-méridien).
lorsque h>180° je me sers de h (anté-méridien) = 2pi - h pour le calcul des coordonnées x et y précédemment évoquées. Mais on peut utiliser d'autres façons de faire.
à 19 h sidérale h sera égal à 327.8188° + 15° = 342.8188° ou 17.1812° anté-méridien .A 20 h sidérale h sera égal à 357.8188° ou 2.1812° a-m.
A 21 h sidérale h sera égal à 357.8188° + 15° = 372.8188° <=> 12.8188° post-méridien.
Et ainsi de suite...
On peut donc dresser un tableau de toutes les valeurs de ces angles horaires de début de signes zodiacaux pour chaque heure sidérale. Puis ne retenir que les valeurs compatibles avec les heures d'ensoleillement du cadran (et sa taille).
Un programme gw basic permet de trouver ces angles horaires.
Remarque: si un angle horaire donne des x,y hors du cadran on peut faire varier la longitude écliptique en plus ou en moins pour essayer de trouver un point plus favorable au tracé de la même heure sidérale.
b) tracé par les points remarquables.
b1- Points sur la méridienne.
Sur la figure 1' est représentée la 18è heure sidérale avec g se levant sur le point cardinal Est et g' se couchant sur le cardinal Ouest (w). 6 heures après nous nous trouvons dans le cas de la 24è heure sidérale ou 0 heure sidérale. g passe au méridien et g' à l'anti-méridien.
g parcourt ensuite l'équateur céleste et nous prenons le cas de la 1ère ou 2è ou3è heure sidérale... Pour la 1ère heure nous aurons l'arc gEq égal à 15°. Pour la 2è heure gEq = 30° etc... On sait que dans un triangle sphérique rectangle le rapport de la tangente d'un côté de l'angle droit à la tangente de l'angle opposé est égal au sinus de l'autre côté de l'angle droit. Le triangle EcEqg rectangle en Eq permet alors d'écrire:
tg EcEq / tg EcgEq = sin Eq g
EcEq étant la déclinaison d du point de l'écliptique passant au méridien à l'heure sidérale considérée, gEq étant l'ascension droite a de gamma c'est-à-dire son angle horaire et l'angle EcgEq étant l'angle epsilon entre l'équateur et l'écliptique.
On a donc tg d = tg e sin a
En septembre 2010 e est proche de 23.4378°. En faisant varier a de 0 à 345° on trouve les valeurs suivantes pour d:
Heure sidérale ____________angle horaire de g en °____________d en °
_____0 (24)_____________________0________________________0
_____1 ________________________15______________________6,402
_____2_________________________30______________________12,230
_____3_________________________45______________________17,042
_____4_________________________60______________________20,578
_____5_________________________75______________________22,721
_____6_________________________90______________________23,4378
_____7_________________________105_____________________22,721
_____8_________________________120_____________________20,578
_____9_________________________135_____________________17,042
_____10________________________150_____________________12,230
_____11________________________165_____________________6,40
_____12________________________180_____________________0
_____13________________________195_____________________-6,4
_____14________________________210_____________________-12,230
_____15________________________225_____________________-17,042
_____16________________________240_____________________-20,578
_____17________________________255_____________________-22,721
_____18________________________270_____________________-23,4378
_____19________________________285_____________________-22,721
_____20________________________300_____________________-20,578
_____21________________________315_____________________-17,042
_____22________________________330_____________________-12,230
_____23________________________345_____________________-6,402
_____24 (0)_____________________360_____________________0
Ce tableau montre que les heures de rang symétrique par rapport à la 6è ou à la 18è lors de leur passage au méridien correspondent à des points d'écliptique ayant même déclinaison. Par exemple la 5è et 7è, la 4è et la 8è, la 17è et la 19è, la 16è et la 20è etc...
Au méridien la hauteur de ces points est égale à pi/2 - f + d où f est la latitude du lieu. Donc les heures symétriques par rapport à 18 h sidérale ou 6h sidérale s'entrecroisent sur la méridienne à cette même hauteur. La connaissance de cette propriété est un bon moyen pour augmenter la précision de leur tracé.
La 6è tangente l'arc diurne du tropique du Cancer sur la méridienne alors que la 18è y tangente l'arc du tropique du Capricorne.
b2- Points sur les solstices.
1heure aprés être passé au méridien le point C de début du capricorne se trouve sur l'heure sidérale suivante c'est-à-dire à 19 h sidérale (fig 2).
fig 2
Ce point est alors sur le cercle horaire correspondant à la 13è heure solaire (1ère heure aprés le passage au méridien). 1 heure encore aprés, à la 20è heure sidérale ce point sera sur le cercle horaire de la 14è heure solaire. De même 1 heure avant 18 heure sidérale, à 17 heure sidérale, on trouvait ce point sur la 11è heure solaire (1 heure avant le passage au méridien).
Il y a donc passage de la 19 è heure sidérale par le point commun au solstice d'hiver (arc diurne du Capricorne) et au cercle horaire de la 13è heure solaire. De même passage de la 20è par le point commun à ce même solstice et au cercle horaire de la 14 è heure solaire. Etc...
A 6 heure sidérale le début du Cancer passe au méridien. c'est le coucher de g et le lever de g ' au point Est. Par le même raisonnement que ci-dessus on pourra dire que la 7 è heure sidérale passe par le point commun au solstice d'été (arc diurne du tropique du cancer) et à la 13 è heure solaire; que la 8è heure sidérale passe par le point commun de ce solstice avec le cercle horaire de la 14 è heure solaire; que la 5 è heure sidérale passe par le point commun de ce solstice avec le cercle horaire de la 11 è heure solaire etc...etc...
b3- Points sur l'équinoxiale.
Regardons la figure 3 où est représentée une sphère céleste à 18 heure et 6 heure sidérale. Dans ces 2 cas l'écliptique et l'équateur céleste ont leur intersection sur le grand cercle de l'horizon.
è
fig 3---------------------------------------fig 4
Ici le point Est des levers est seul représenté mais il en va de même pour le point Ouest. Cette intersection commune se fait pour les levers sur le cercle horaire correspondant à la VI è heure solaire (du matin correspondant à l'angle horaire 270°). 1 heure plus tard cette intersection va se faire sur le cercle horaire suivant correspondant à la VIIè heure solaire et on sera alors dans la configuration des heures sidérales suivantes c'est-à-dire 7 ou 19. Donc tout au long de l'équateur céleste et sur le cadran son image gnomonique, c'est-à-dire l'équinoxiale, les heures sidérales s'entrecroisent avec leurs opposées.
Le point commun à la 6è et 18è coupant l'horizon Est sur VI heure solaire du matin et l'horizon Ouest sur VI heure solaire du soir. On voit très bien cela sur le cadran à queue de chat sur le site exposé.
Ensuite les 7è et 19è se couperont sur l'équinoxiale à sa rencontre avec la VIIè heure solaire du matin, puis 8è et 20è avec la VIIIè, 9è et 21è avec la IXè, 10è et 22è avec la Xè,....,les 12è et 24è (0) se coupant au croisement de la méridienne avec l'équinoxiale.....etc....
Ainsi, à partir de quelques points communs et remarquables il nous sera possible de tracer assez facilement un cadran solaire à heures sidérales.
2- Lecture du cadran
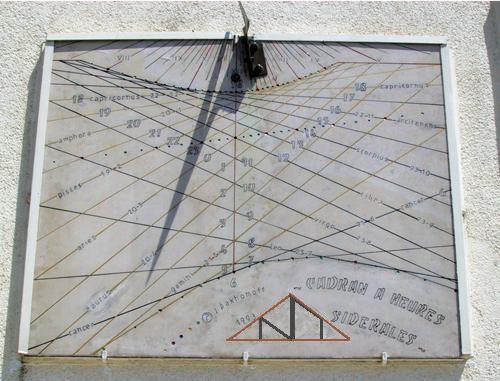
La lecture de l'heure sidérale, une fois ces heures tracées sur le cadran, peut sembler quelque peu difficile. En effet, comme il en est pour les arcs diurnes zodiacaux avec les dates, chaque point du cadran peut correspondre à deux heures différentes. Ainsi la photo ci-dessus montre le bout du style près de 3 heures ou de 7 heures.
Il nous faudra donc savoir comment retenir la bonne heure. Pour cela nous calculerons pour une latitude correspondante à celle de l'implantation du cadran et pour un temps sidéral donné (que nous ferons varier de 0 à 23 heures) l'ascendant, le nonagésime et le descendant sur l'horizon du cadran. Nous nous aidons pour cela du programme, après l'avoir quelque peu simplifié, employé dans la domification de Régiomontanus.
Pour un horizon de latitude nord 46°, correspondant à la latitude moyenne de la France, avec epsilon égal ce 11 septembre 2010 à 23.4379° nous obtenons les nonagésimes suivants :
0h sidérale _________Nonagésime = 22,38° Bélier
1h sidérale ________Nonagésime 33.91° Taureau
2h sidérale _________Nonagésime 45.15° Taureau
3h ________________Nonagésime 56.3° Taureau
4h _________________________67.48° Gémeaux
5h__________________________78.72° Gémeaux
6h__________________________90° Cancer
7h__________________________101.27 ° Cancer
8h__________________________112.51 ° Cancer
9h__________________________ 123.69° Lion
10h__________________________134.84° Lion
11h__________________________146.08° Lion
12h__________________________157.61° Vierge
13h__________________________169.76° Vierge
14h__________________________183.09° Balance
15h__________________________198.52° Balance
16h__________________________217.42° Scorpion
17h__________________________241.38° Sagittaire
18h__________________________270° Capricorne
19h__________________________298.61° Capricorne
20h__________________________322.57° Verseau
21h__________________________341.47° Poissons
22h__________________________356.9° Poissons
23h__________________________10.23° Bélier
On voit que les heures sidérales de la 12è à la 24è correspondent aux signes zodiacaux de l'automne et de l'hiver passant vers la mi-journée dans les zones hautes du ciel diurne.
De même les heures sidérales de la 0 à la 11è correspondent aux signes zodiacaux du printemps et de l'été passant vers la mi-journée dans lez zones méridiennes (hautes du ciel diurne).
On pourra en conclure que sur le cadran les heures 0 à 11 correspondront aux déclinaisons positives du printemps et de l'été et que les heures 12 à 24 correspondront aux déclinaisons négatives de l'automne et de l'hiver.
En hiver c'est l'heure 18 qui fera référence car nonagésime et milieu du ciel s'intercepteront sur la méridienne: les heures lues seront proches et de part et d'autre de 18.
En été c'est la 6è heure qui fera référence car nonagésime et milieu du ciel s'intercepteront également sur la méridienne: les heures lues seront proches et de part et d'autre de 6.
Au printemps g sur l'équateur sera au méridien à 0 heure sidérale. C'est donc cette heure 0 qui fera référence au printemps: les heures lues seront proches et de part et d'autre de 0.
A l'automne g' sur l'équateur se trouvera au méridien à 12 heure sidérale. C'est donc cette heure 12 qui fera référence à l'automne: les heures lues seront proches et de part et d'autre de 12.
Lieu géométrique du nonagésime
(dossier pdf: attendre quelques instants son ouverture)
retour au cadran à heures sidérales des Caillols
Latitude 43° 21' 4'' nord
Longitude -5° 24' 50'' est
Déclinaison gnomonique
-------------54° 50' 13'' nord est (234° 50' 13'')

>