 Fig 1
Fig 1
Transformation des arcs cosinus et sinus
en arcs tangentes
Jean Pakhomoff
Si x=cos a il existe une quantité B fonction de x telle que arc tangente B = a.
L'exécutable gwbasic utilisé entre autre dans mes programmes de cadrans solaires donne, connaissant la valeur de la tangente d'un arc a,
directement la valeur de l'arc tangente a. Il ne donne pas par contre directement la valeur des arcs à partir de leur sinus ou cosinus.
Il nous faudra par conséquent trouver une nouvelle quantité, à partir de la valeur du sinus ou du cosinus, égale à la valeur de la tangente de l'arc considéré
pour connaître la grandeur de cet arc.
Nous utiliserons pour cela un simple procédé géométrique. Le terme sqr signifie "racine carrée de" .
Soit l'arc de valeur a radians.
1- Cas de l'arc cosinus.
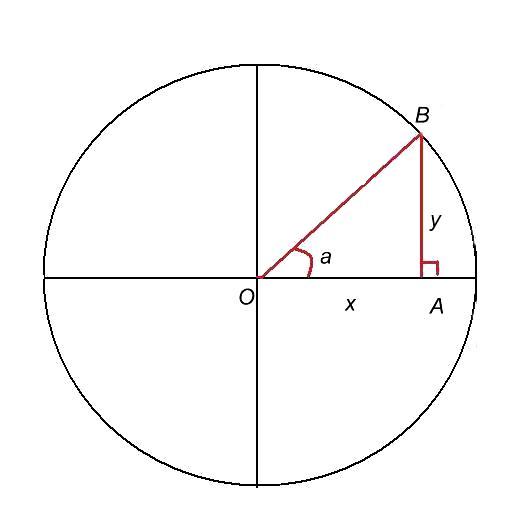
a) 0<a<pi/2 - figure 1
 Fig 1
Fig 1
On a x = cos a et tg a = AB/x ; AB²+x² = OB² = 1 et AB = sqr(1-x²) d'où tg a = sqr(1-x²) / x avec x = cos a et l'ordinateur donne
l'arc tangente de sqr(1-x²) / x c'est-à-dire a = arctg (sqr(1-x²) / x)
b) pi/2<a<pi - figure 2
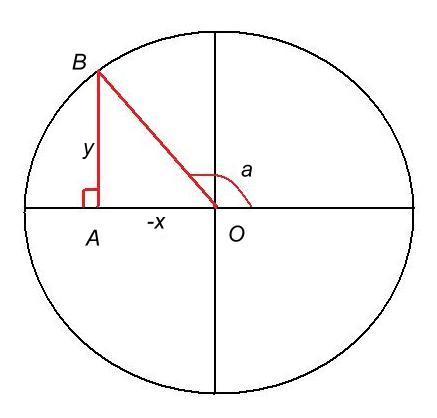 Fig 2
Fig 2
cos a étant <0 on prendra OA = -x et tg (pi-a) = AB/OA = AB/-x. De même (-x)² + AB² = 1 => AB = sqr(1-x²)
tg (pi-a) = sqr(1-x²) / -x => pi-a = arctg (-sqr(1-x²) / x) = - arctg (sqr(1-x²) / x) et
a = pi + arctg (sqr(1-x²) / x)
c) pi<a<3pi/2 - figure 3.
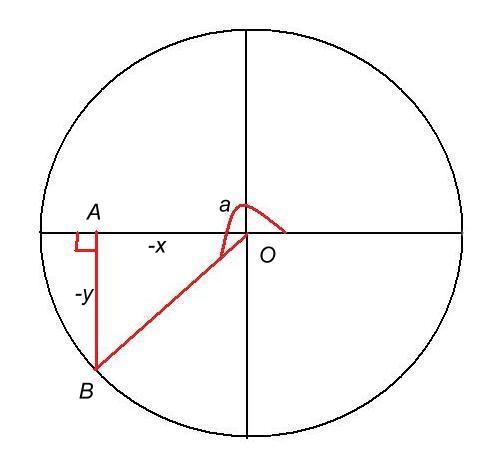 Fig 3
Fig 3
cos a étant <0 on prendra OA = -x et tg (a-pi) = AB/OA = AB/-x. De même (-x)² + AB² = 1 => AB = sqr(1-x²)
tg (a-pi) = sqr(1-x²) / -x => a-pi = arctg (-sqr(1-x²) / x) = - arctg (sqr(1-x²) / x) et
a = pi - arctg (sqr(1-x²) / x)
d) 3pi/2<a<2pi - figure 4
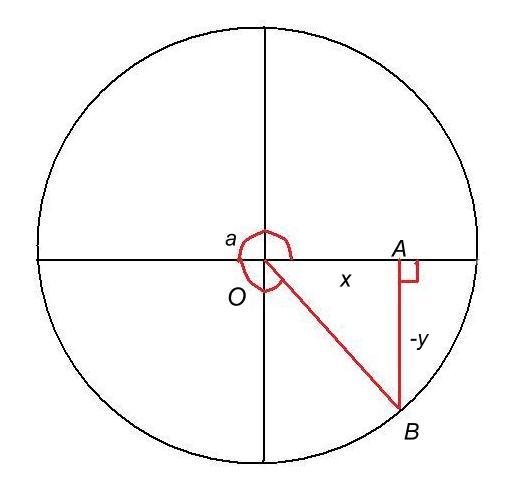 Fig 4
Fig 4
cos a = x et tg (2pi-a) = AB/OA = AB/x. De même (x)² + AB² = 1 => AB = sqr(1-x²)
tg (2pi-a) = sqr(1-x²) / x => 2pi-a= arctg (sqr(1-x²) / x) et
a = 2pi - arctg (sqr(1-x²) / x)
2 - Cas de l'arc sinus.
a) 0<a<pi/2 - figure 1
On a y = sin a et tg a = y/x ; OA²+y² = OB² = 1 et OA = sqr(1-y²) d'où tg a = y/sqr(1-y²) avec y = sin a et l'ordinateur donne
l'arc tangente de x/sqr(1-y²) c'est-à-dire a = arctg (y / sqr(1-y²))
b) pi/2<a<pi - figure 2
sin a = y et tg (pi-a) = AB/OA = y/x. De même (y)² + OA² = 1 => OA = sqr(1-y²)
tg (pi-a) = y / sqr(1-y²) => pi-a = arctg (y / sqr(1-y²)) et
a = pi - arctg (y / sqr(1-y²))
c) pi<a<3pi/2 - figure 3
ici le sinus étant négatif on prendra AB = - y et tg (a-pi) = AB/OA = -y/OA. De même (-y)² + OA² = 1 => OA = sqr(1-y²)
tg (a-pi) = -y / sqr(1-y²) => a-pi = arctg (-y / sqr(1-y²)) = - arctg(y/sqr(1-y²)) et
a = pi - arctg (y / sqr(1-y²))
d) 3pi/2<a<2pi - figure 4
le sinus étant là aussi négatif on prendra AB = - y et tg (2pi-a) = AB/OA = -y/OA. De même (-y)² + OA² = 1 => OA = sqr(1-y²)
tg (2pi-a) = -y / sqr(1-y²) => 2pi-a = arctg (-y / sqr(1-y²)) = - arctg(y/sqr(1-y²)) et
a = 2pi + arctg (y / sqr(1-y²))
Lorsque la calculette donne directement l'arc sinus ou cosinus, comme par exemple la casio FX702-P les corrections sont différentes.
Connaissant le quadrant dans lequel nous devons nous trouver nous procédons ainsi:
a) Cas du cosinus:
entre 0 et PI aucune correction à apporter.
entre PI et 2PI la machine donne l'arc correspondant entre 0 et PI. Donc il faut négativer le résultat et ajoutter 2PI.
exemples: cos 120 = -0.5 et arccos -0.5 = 120
cos 240 = -0.5 et arc 0.5 = 120 . On prend donc -120 + 360 = 240
cos 330 = 0.8660254038 et arc 0.8660254038 = 30 . On prend -30 + 360 = 330 ........
b) Cas du sinus:
Entre PI/2 et 3PI/2 la machine donne l'arc le plus petit par rapport à l'axe des y. On prend donc ce résultat et on le soustrait à PI.
Exemples:
sin 120 = 0.8660254038 et arc sinus 0.8660254038 = 60 . On prend 180 - 60 = 120.
sin 200 = -0.3420201433 et arc sinus -0.3420201433 = -20 . On prend pareillement 180 - (-20) = 200
Entre 3PI/2 et 2PI la machine donne l'angle négatif correspondant. On le soustrait donc à 2PI.
Exemple: sin 300 = -0.8660254038 et arc sinus -0.8660254038 = -60 . On prend 360 + (-60) = 300
Retour à la domification de Régiomontanus
Retour à mes travaux personnels