La courbe d'équation du temps
sur un cadran solaire
Jean Pakhomoff
Nous donnons ici quelques explications sur la signification des courbes en 8 allongées que l'on trouve sur les cadrans solaires.
Un cadran solaire paraît être presque toujours en retard ou en avance sur l'heure civile.
S'il est gradué en heures solaires il y a tout lieu de penser que les passants n'y font pas attention car ,
sauf dans des cas de longitudes bien favorables, l'heure du cadran est éloignée tous les jours de l'heure de la montre.
Si par contre le cadran est tracé en heures civiles l'avance ou le retard sera alors plus facilement appréciable car l'heure
donnée par le cadran est proche de l'heure donnée par la montre.
1) Temps sidéral.
C'est le temps en rapport avec la rotation du globe terrestre ou de la sphère des fixes.
La sphère céleste, suite au mouvement diurne de la terre, fait un tour sur elle-même en 24 heures sidérales.
Et de même tous les éléments qui la composent y compris les points Gamma et Gamma' intersections du grand cercle
de l'équateur céleste ,sur lequel se comptent les ascensions droites, et de l'écliptique sur lequel se comptent les
longitudes écliptiques du soleil.
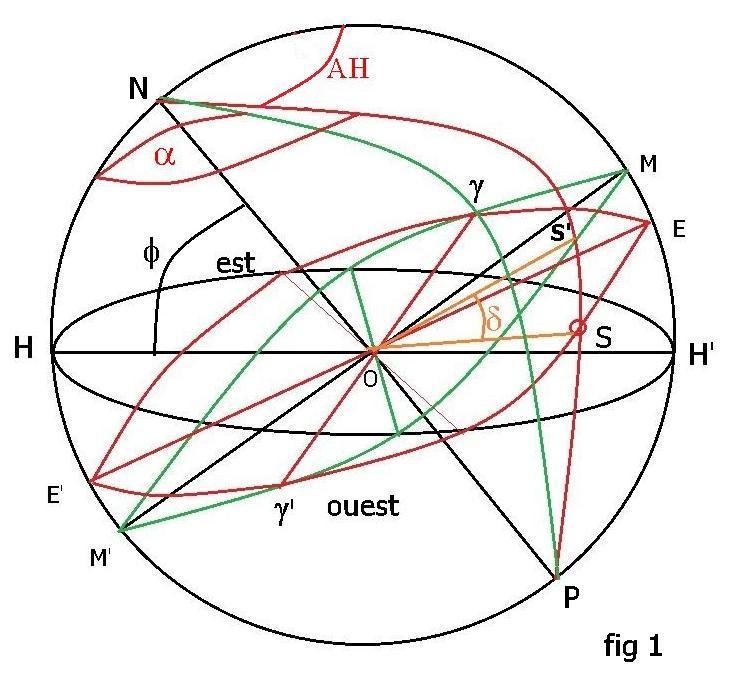
La figure 1 représente une sphère céleste vue du côté ouest de l'horizon. Nous voyons l'équateur céleste coupant
le grand cercle méridien en MM' ; l'écliptique coupant ce même cercle en EE' et les points Gamma Gamma' intersection
de l'équateur et de l'écliptique. L'axe des pôles perpendiculaire à l'équateur fait un angle F avec le grand cercle de l'horizon.
On a représenté le soleil à l'ouest en S sur le grand cercle écliptique. Par S passe le cercle horaire NSP d'angle horaire AH.
La déclinaison d du soleil correspond sur ce cercle horaire à l'angle SOS'.

On dit qu'il est 0 heure sidérale quand le point Gamma g passe en M au méridien du lieu.
On tire de la simple observation la relation TS = AR + AH : le temps sidéral est égal à la somme de l'ascension
droite a (Ascensio Recta) d'une étoile quelconque et de son angle horaire AH.
Entre 2 passages du point G au méridien il s'écoule 24 heures sidérales.
2) Temps solaire vrai.
C'est le temps réel. L'heure juste du cadran solaire. L'heure de la nature. Il est midi lorsque le soleil passe au méridien.
3) Temps solaire moyen.
Le soleil passe au méridien avec des écarts de temps pouvant atteindre la demie-heure selon les époques de l'année.
Le cadran sera en avance de 16 minutes début novembre et en retard de 15 vers la mi-février.
Ces écarts sont rassemblés dans ce qu'on appelle l'équation du temps. Nous verrons ci-dessous que la valeur de cette
équation du temps est égale à la somme de 2 valeurs variables l'une appelée équation du centre et l'autre la réduction à l'équateur.
Il a donc été nécessaire de créer un temps solaire moyen de 24 heures égales.
On se sert pour cela d'un soleil moyen fictif, proche du soleil réel situé lui sur l'écliptique, parcourant l'équateur céleste
tout au long de l'année en partant de Gamma et se retrouvant au point Gamma aprés une durée de 1 an.
L'observation a montré que ce retour en Gamma se faisait exactement aprés 336,2422 passages de Gamma
au méridien du lieu de départ initial.
Le soleil fictif ayant pendant ce temps là avancé sur l'équateur de son mouvement propre dans le sens contraire
à Gamma aura alors fait un passage de moins à l'arrivée au méridien.
La figure 2 montre cela sur un exemple simple. Soit une jante de bicyclette et sa valve en V.
Sur l'entrée de la valve se trouve un petit hamster A. A l'instant t la jante se met à tourner dans le sens des aigilles
d'une montre et le hamster parcourt alors la jante en sens inverse de telle façon que lorsque la valve a fait un tour
complet de 2 pi le hamster a parcouru pi/2 en sens inverse.
Au départ V et A sont confondus. Au premier tour de V, A ne paraît avoir fait que 3/4 de tour dans le mouvement de V;
au 2è tour de V, A a fait un tour et 1/2; au 3è tour A a fait 2 tours 1/4 et au 4è tour le soleil a fait un tour de moins c'est-à-dire 3 tours.
C'est ce qui se passe pareillement lorsque la valve V devient Gamma et le hamster A le soleil.
L'angle de déplacement de A dans le sens inverse de V n'étant plus pi/2 mais 0.98564583°.
On pourra alors dire que 366,2422 jours de temps sidéral équivalent à 365,2422 jours de temps solaire moyen d'où
1 jour solaire moyen = 366,2422/365,2422 = 1.002737909 jour sidéral = 24 h sidérales + 3'56,555'' sidérales.
Ces 3'56,555'' de temps sidéral correspondent au temps de retard pris par le soleil moyen équatorial
sur gamma chaque fois que Gamma passe au méridien.
1 degré sur l'équateur valant 4' de temps ce temps équivaut donc à un angle de 3'56,555 / 4 = 0.98564583°
Cette valeur angulaire sera appelée moyen mouvement n du soleil fictif sur l'équateur céleste.
On affine cette valeur en considérant le rapport la valeur de l'année tropique en jours avec la circonférence
de l'équateur ce qui donne 360° / 365.2422 jours = 0.9856473321°. Cette valeur de n sera retenue par la suite.
4) Variation due à l'équation du centre.
Cette valeur moyenne varie selon la position de la terre sur son orbite dans des valeurs comprises entre 1,02°
vers le 2 janvier (vitesse rapide prés du périhélie) et 0,952° début juillet (vitesse lente vers l'aphélie) donnant
en conséquence des avances ou retards plus ou moins importants par accumulation journalière de ces différences.
Ces différences entre position du soleil vrai et du soleil moyen s'annulent le 2 janvier et le 2 juillet.
Les valeurs les plus grandes sont atteintes le 3 avril avec un angle de + 1°55' (avance du soleil vrai sur le soleil moyen)
et le 1er octobre avec -1°55' (retard du soleil vrai). Approximativement ces valeurs correspondent à une sinusoïde
d'équation C = 1.9166666 sin nt
où C est la valeur de l'équation du centre, n le moyen mouvement égal à 0.98564583° et t le nombre de jours à compter
du passage de la terre au périhélie. 1°55' = 1.9166666°. Ce passage avait lieu le 1er janvier 1900 et la longitude du soleil
était alors de 281.2187°
5) Variation due à la réduction à l'équateur.
Chaque variation journalière en longitude sur l'écliptique donne lieu à une autre variation sur l'équateur en ascension droite.
C'est cette dernière qui va directement influer sur la valeur de l'angle horaire du soleil comme nous l'avons vu ci-dessus
(TS=AR+AH). Or pour des déplacements identiques en longitude écliptique on obtient des déplacements inégaux en ascension droite.
Une relation simple lie l'ascension droite a et la longitude écliptique l : ....tg a = tg l cos e...où e est l'angle fait entre
l'écliptique et l'équateur céleste proche de 23.44°.
Dressons le tableau ci-dessous qui montre que pour des déplacements égaux en longitude on obtient des variations inégales
de l'ascension droite:
.........l.................... ...a....................delta a
.......20° ..................21.64°.......
.......30.....................27.9...................6.26
.......40.....................37.58.................9.68
.......50.....................47.55.................9.97
.......60.....................57.81.................10.26.....etc...
Montrons comment l'on obtient la relation tg a = tg l cos e
Soit la sphère céleste de centre o représentée ci-dessous à 6 h sidérale. Le point gamma G ou point vernal se couche à l'horizon ouest.
L'axe des pôles OP et le pôle écliptique Pe.
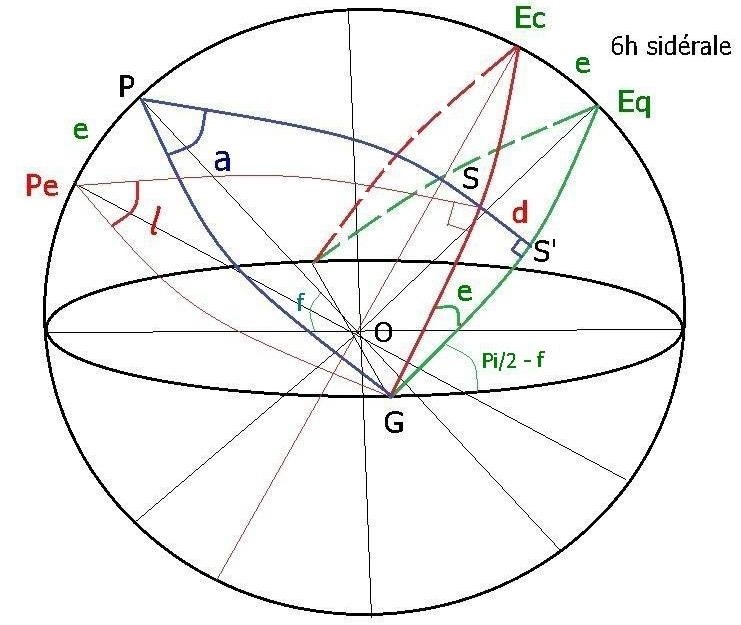
e l'angle d'inclinaison de l'équateur céleste de couleur verte sur l'écliptique de couleur rouge.
GS' l'ascension droite a du soleil en S,
GS la longitude écliptique l de celui-ci et SS' = d la déclinaison de S.
GSS' rectangle en S' nous permet d'écrire: tg d / tg e = sin a .et tg d = tg e sin a..... (1)
On a également cos l = cos d cos a + sin d sin a cos pi / 2 et cos l = cos d cos a.....(2)
de même sin (pi / 2) / sin l = sin e / sin d d'où sin l = sin d / sin e.....(3)
Divisons (3) par (2) on obtient tg l = (sin d / sin e) / cos a cos d = tg d / sin e cos a, en remplaçant tg d
par sa valeur (1) on a tg l = tg e sin a / sin e cos a ce qui fait en définitive
tg l = tg a / cos e et tg a = tg l cos e (4)
La tangente de l'ascension droite est égale au produit de la tangente de la longitude par epsilon.
Cependant si cette relation permet de connaître l'ascension droite du soleil à partir de sa longitude elle ne
renseigne pas immédiatement sur la variation journalière de cette ascension droite en fonction de la position
du soleil sur l'écliptique à une date précise de sa trajectoire.
Il nous faut apprécier la différence angulaire entre la longitude du soleil à une date donnée et la correspondance
en ascension droite sur l'équateur.
Cette différence sera la valeur de la réduction à l'équateur qui modifiera d'autant l'ascension droite du soleil selon sa longitude.
Pour cela écrivons dans (4) cos e en fonction de l'arc moitié. Nous aurons en appelant tg e/2 = t , cos e = (1-t²) / (1+t²)
et tg a = tg l (1-t²) / (1+t²) => tg a + tg a t² = tg l - tgl t² => tg a - tg l = - t² (tg a + tg l) =>
sin a / cos a - sin l / cos l = - t² (sin a / cos a + sin l / cos l) ==> sin a cos l- sin l cos a = - t² (sin a cos l + sin l cos a) ==>
sin (a - l) = - t² sin (a + l) ; la valeur maximum de sin (a + l) étant 1 la valeur absolue de sin (a-l) est t² <==> tg² (23,45/2) =
0,208² = 0,0431 ce qui correspond à un angle de 2° 28' <==> 148' d'arc.
Cet angle étant petit on peut l'identifier à son sinus (en radian) et donc dire que sin (a - l) = - 148' sin (a + l) = a - l ;
a étant toujours proche de l on pourra simplifier en écrivant
a - l = - 148' sin 2l = R-- C'est l'expression de la réduction à l'équateur différence entre l'ascension doite équatoriale et la longitude
du soleil pour la longitude l.
On obtient l'heure civile en corrigeant l'heure solaire moyenne de la valeur de l'équation du temps et de celle de la longitude géographique).
En fin de compte l'heure solaire moyenne va varier tous les jours avec l'heure vraie du soleil de la valeur E de l'équation du temps qui est la
somme des 2 variations étudiées (pour l'essentiel). On aura donc
E = C + R = 115' sin nt - 148' sin 2 l .
1' d'angle équivaut à 4'' de temps d'où en temps E = 460 sin nt - 592 sin 2 l---
Variation de l'équation du temps au cours du temps.
On prend pour origine des temps le 1er janvier 1900.
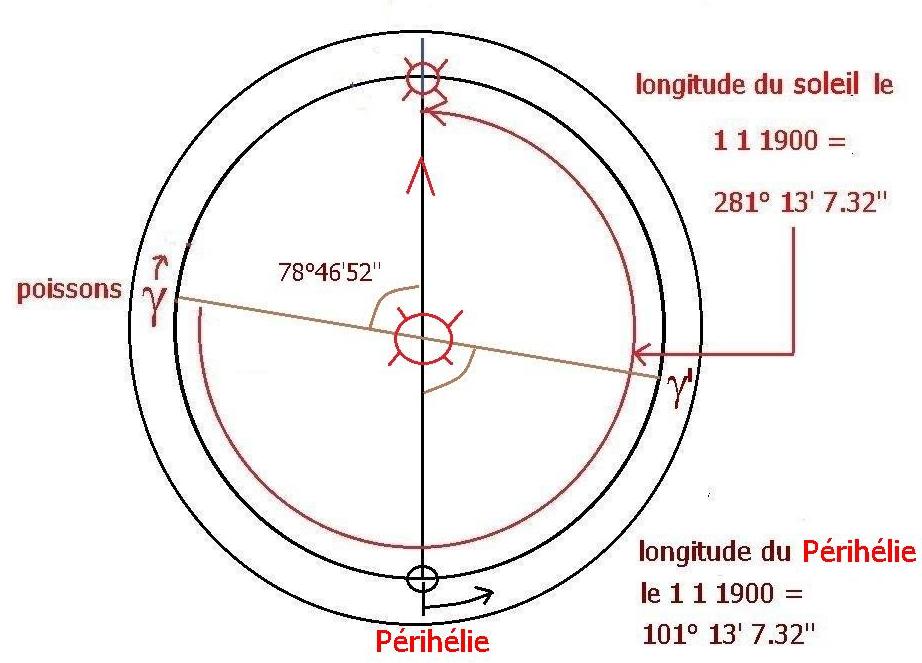
La longitude du soleil était alors celle du périhélie + pi : 101.2187 + 180 = 281.2187°
Le périhélie par son mouvement propre augmente sa longitude de 11.461'' d'arc chaque année et le point vernal
gamma origine des longitudes se déplace de 50.256'' d'arc dans le sens rétrograde (précession des équinoxes).
Ces deux mouvements accroissent donc la longitude du périhélie de 61.717'' d'arc ou de 0.0171436° chaque année.
Au bout de 1000 ans la longitude du périhélie aura augmenté de 61717/3600 = 17.1436° ce qui correspond à
17.1436/0.9856473321 = 17.393 jours
0.9856473321 étant le moyen mouvement journalier de la terre ou du soleil.
L'origine des temps ne sera donc plus au 1er janvier mais au 17 janvier
et ainsi de suite pour les siècles et millénaires suivants...au bénéfice d'une légère approximation vu que d'autres
causes naturelles de mondre importance jouent sur le mouvement du périhélie.
Par exemple le périhélie et le point gamma' seront confondus dans 4595,37 ans après 1900.
Le soleil se trouvant alors au point gamma le jour du printemps à l'aphélie opposé au périhélie celui-ci se trouvant
en gamma' le jour de l'automne vers le 21 septembre de l'année 6495: (360 - 281.2187) / 0,0171436 = 4595,37.
Il faudra tenir compte de cela dans le calcul des valeurs de l'équation du temps.
On appelle Z le gain en longitude du périhélie depuis le 1 1 1900.
On posera Z = 0.0171436° X A où A représente la différence entre l'année pour laquelle on calcule l'équation du temps et l'année 1900.
Z divisé par la valeur du moyen mouvement donne le nombre de jours correspondant au déplacement du périhélie.
C'est donc cette nouvelle date qui va correspondre à l'origine des incrémentations nt des longitudes.
On calcule alors l'équation du temps à partir de cette longitude 281.2187 + Z et on rectifie les dates par le moyen utilisé dans le programme
basic joint à la fin de ce travail.
On obtiendra la longitude du soleil pour le calcul de E par la formule ci-dessous déduite des considérations ci-dessus:
l = 281.2187 + Z + nt + 1.9166666 sin nt
où n est le moyen mouvement égal à 0.9856473321° et t le nombre de jours depuis le Zè jour.
En fin de compte l'équation du temps peut s'écrire
E = 460 sin nt - 592 sin 2 (281.2187 + Z + nt + 1.9166666 sin nt)
L'équation du temps a en ce début de XXIè siècle 4 maximums: le soleil avance de 16'23'' le 4 novembre, de 3'47'' le 15 mai.
Son retard est de 14'22'' le 11 février et de 6'23'' le 27 juillet. A quelques secondes prés.
En transformant les valeurs de l'équation du temps en angles horaires on peut tracer celle-ci sur les cadrans solaires.
Il est l'heure de la ligne horaire sur laquelle elle est construite lorsque l'ombre du point stylaire la touche à la date de lecture.
Pour terminer montrons les variations des 3 quantités étudiées au cours de l'année sur un graphique tiré de
l'Astronomie Générale de Bakouline Kononovitch et Moroz (Editions Mir de Moscou):
...quelques courbes d'équation du temps réalisées sur différents cadrans solaires.
sur un cadran septentrional
sur la méridienne d'un bifilaire horizontal
sur un vertical à polo (1h 30) et sur un bifilaire
vertical qui lui est perpendiculaire (11h 45)
sur midi solaire d'un vertical avec
également la courbe graphique
J'ai tiré des calculs ci-dessus le progamme informatique ci-dessous qui permet de connaître les valeurs de E chaque jour de l'année
avec une trés bonne approximation. Je donne aussi un programme permettant le passage de l'heure lue au cadran à l'heure civile et inversement.
bibliographie:
Cours d'astronomie Georges Faure Société Flammarion Marseille 1986
André Danjon -Astronomie Générale Editions Albert Blanchard 1980
L' Astronomie Générale de Bakouline Kononovitch et Moroz (Editions Mir de Moscou)
Traité de Cosmographie de A. Grignon Editions Vuibert et Nony - Paris 1904
Programme informatique pour le calcul de l'équation du temps
Retour à mes travaux personnels
Equation de Képler et équation du centre