Eléments de cosmographie
utilisés en gnomonique

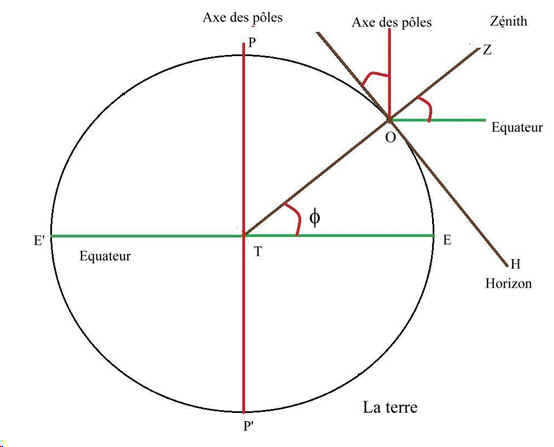
fig 1
La figure 1 représente la terre avec l'axe des pôles PP' perpendiculaire à un diamètre de l'équateur terrestre EE'.
On choisit un horizon H de latitude f dont l'axe tangente la terre en O. On trace l'axe Zénith Nadir perpendiculaire à l'horizon et passant par le centre T de la terre et le point O.
En traçant à partir du point O une sphère nous retrouvons les éléments définis ci-dessus, tous parallèles à eux-mêmes, comme des grands cercles de la sphère de centre O.
Sur la figure 2 sont tracés ces grands cercles: grand cercle de l'horizon, de l'équateur, l'axe OZ étant l'axe du 1er vertical passant par les points cardinaux Est (E) et Ouest (W).
Les points N P Z E' S P' E'' définissent le méridien de l'horizon H (NESW) de centre O.
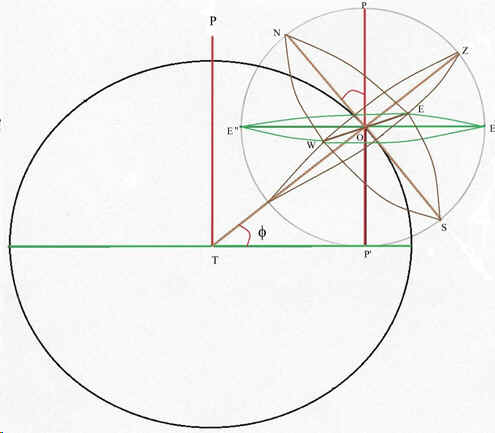
fig 2
Représentons sur la figure 3 cette sphère céleste à 18h sidérale. Cela correspond au lever du point g au point cardinal Est sur l'horizon.
6 heures plus tard ce point passera au méridien PS et le point Q sera en W, C en W', W en Q', C' en C'' et E en Q.
L'équateur EQWQ' est représenté en vert faisant un angle e égal à environ 23°45' avec le grand cercle ECWC' de l'écliptique porteur du zodiaque qui est représenté en rouge.
Nous aurons l'occasion d'étudier dans les paragraphes suivants la variation d' e au cours du temps.
L'axe des pôles PP' perpendiculaire à l'équateur céleste est dans le plan méridien comme l'est l'axe de l'écliptique perpendiculaire au plan de l'écliptique.
L'angle P O Pec = e à 18 h sidérale comme à 6h sidérale fait entre le pôle de l'équateur et le pôle de l'écliptique est dans le plan méridien.
L'axe des pôles de l'équateur céleste est le diamètre commun aux cercles horaires tous perpendiculaires à l'équateur.
C'est à partir de l'équateur céleste que seront comptées les déclinaisons d et ascension droite a des différents objets célestes permettant leur localisation sur la sphère céleste.
L'angle PON est égal à la latitude f.
L'axe Zénith Nadir ZZ' perpendiculaire à l'horizon est le diamètre des grands cercles verticaux permettant de connaître la hauteur h et l'azimut A des objets célestes au-dessus de l'horizon.
A partir de l'axe des pôles de l'écliptique et de l'écliptique seront comptées les longitudes l et latitudes écliptiques ß des objets célestes.
Ce dernier système de coordonnées écliptiques indispensable pour les calculs astronomiques est d'un moindre intérêt pour le gnomoniste.
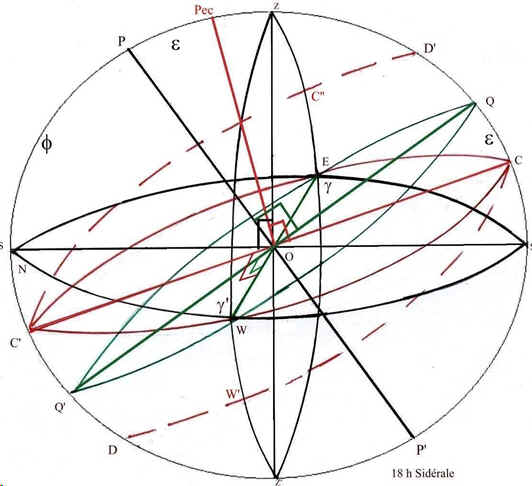
fig 3
Représentons maintenant la sphère céleste lorsque le diamètre gg' n'est pas confondu avec l'horizon, ce qui est les cas général. Choisissons le cas de la figure 4.
g a suivi son arc diurne et parcuru 45° comme Q, g' et Q'. Il est environ 18+3 = 21 h sidérale.
Le point P est toujours dans le plan méridien alors que le point Pec décrit un cercle base d'un cône de révolution d'ouverture 2 e de sommet O dont la directrice est l'axe OP
et la génératrice l'axe OPec.
L'angle horaire t est égal au déplacement de g sur l'équateur.
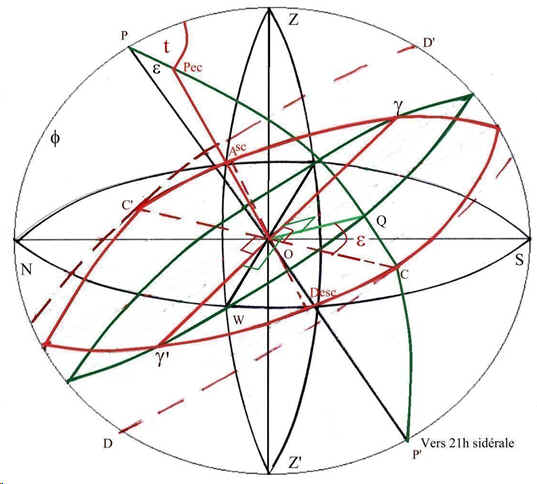
fig 4
Cet angle t correspond a une quantité de temps sidéral rendant compte d'une durée de rotation de la sphère céleste.
La rotation de la sphère se faisant en 24 heures sidérales on divise cette sphère en 24 fuseaux égaux chacun à 15° ou 1 heure de temps sidéral.
C'est pourtant ces fuseaux qui renseigneront sur l'heure solaire des cadrans solaires par leurs traces sur les plans des cadrans.
Ces fuseaux et donc les lignes horaires tabulaires des cadrans ne rendent pas compte de l'heure solaire mais de l'heure sidérale en rapport avec la course du point g sur l'équateur céleste.
Le soleil se déplaçant sur l'écliptique ne passera pas toujours au même moment au méridien et l'heure solaire vraie lue au cadran variera quelque peu chaque jour.
Nous verrons dans le chapitre consacré à l'équation du temps comment lire l'heure légale à partir de l'heure solaire vraie lue sur les lignes horaires des cadrans solaires.
Pour terminer montrons comment se présentent les origines des coordonnées ainsi que la valeur des angles en rapport avec les trois systèmes évoqués ci-dessus.
Nous donnerons quelques formules établies par usage de la trigonométrie sphérique.
La démonstration peut en être trouvée sur tout livre d'astronomie et en particulier sur l'Astronomie Générale de A.Danjon Editions A. Blanchard ou de
P.Bakouline, E. Kononovitch et V. Moroz aux éditions Mir de Moscou. Ces formules permettent de connaître un élément à partir de deux autres et de passer d'un système de coordonnées à l'autre.
- Coordonnées horizontales et équatoriales.
2 cas sont à envisager
L'astre est soit dans l'hémisphère céleste occidental (fig 5) soit dans l'hémisphère oriental (fig 6)
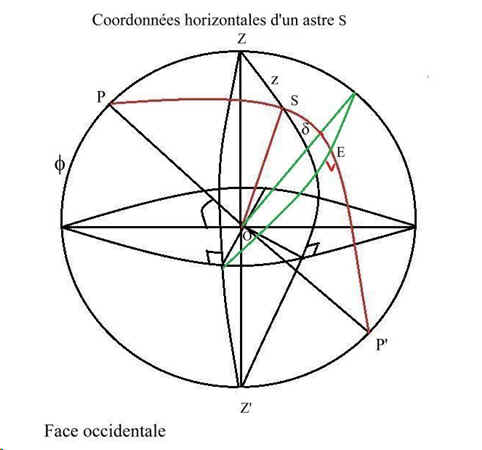
fig 5
L'équateur céleste est en vert le cercle horaire de déclinaison PEP' passant par l'astre S est en rouge.
Ce cercle comme tous les autres cercles horaires est perpendiculaire à l'équateur. Le vertical ZS passant par S est perpendiculaire à l'horizon.
Le rayon OS trace de l'intersection du vertical ZS avec le cercle horaire PSP matérialise le rayon de soleil donnant l'heure sur le cadran solaire quand S représente le soleil.
Il nous faut envisager le triangle sphérique PZS. Le côté PZ est égal à p/2 – f ,
le côté PS est égal à p/2 - d et le côté ZS est égal à z = p/2 - h où h est la hauteur de l'astre sur l'horizon.
PZP'Z' délimitant le plan méridien l'angle SZP' représente l'azimut A de l'astre S. Cet azimut va varier de 0 à 360° à partir du méridien vers l'Ouest .
L'angle PZS est alors égal à p – A.
L'angle ZPS est égal à l'angle horaire t qui varie également de 0 à 360° à partir du méridien vers l'Ouest.
Le côté PZ = p/2 – f et le côté ZS = p/2 – d
Voyons ce que devient ce triangle ZPS sur l'hémi sphère orientale (fig 6).
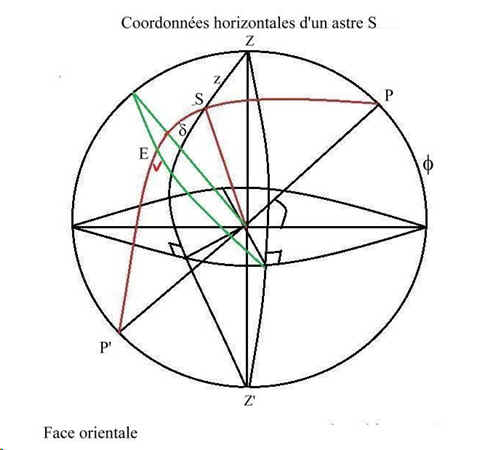
fig 6
Ici on a ZPS = 2 p – t et PZS = p – (2 p – A) = A - p
En appliquant les formules de trigonométrie sphérique évoquées ci-dessus on peut voir que ces deux cas se fondent en des formules uniques car
les différences de signes entraînées par différences d'angles s'annulent.
On obtient finalement en prenant comme initiaux le côté PS et l'angle t ou 2p - t
sin d = sin f cos z – cos f sin z cos A
cos d sin t = sin z sin A
cos d cos t = cos f cos z + sin f sin z cos A
avec f = latitude, d = déclinaison, z = complémént de la hauteur, A = azimut
Ces formules permettent de passer des coordonnées horizontales de l'astre S (en connaissant sa hauteur et son azimut) à ses coordonnées équatoriales
de déclinaison et d'ascension droite.
La connaissance de l'angle horaire t et du temps sidéral ts donne l'ascension droite a :
a = ts – t
En prenant comme initiaux le côté ZS et l'angle p – A ou A - p on obtient
cos z = sin f sin d + cos f cos d cos t ...((1)....cette relation permet de connaître la hauteur h de l'astre puisque z=pi/2 - h:
sin h = sin f sin d + cos f cos d cos t
sin z sin A = cos d sin t .....(2)
sin z cos A = - cos f sin d + sin f cos d cos t.....(3)
En divisant 2 par 3 on obtient la relation donnant l'azimut de l'astre: ...tg A = sin t / (-cos f tg d + sin f cos t)
Pour l'hémisphère sud il convient de considérer la valeur négative de f.
Ces différentes valeurs permettent le calcul des hauteurs, azimuts, des instants de levers et couchers des astres, de la latitude du lieu d'observation.
Leur connaissance est donc capitale en gnomonique.
- Coordonnées équatoriales et écliptiques.
Les coordonnées équatoriales sont la déclinaison et l'ascension droite d'un astre par rapport au grand cercle de l'équateur céleste.
Les coordonnées écliptiques sont la latitude et la longitude écliptique par rapport au grand cercle de l'écliptique incliné d'un angle e égal à 23° 26' sur l'équateur céleste en 2014.
L'origine de ces coordonnées est le point g situé à la rencontre de l'équateur et du méridien 0 de 0h sidérale.
Nous allons ici aussi donner les valeurs de côtés et d'angles du triangle sphérique nécessaire aux calculs de ces coordonnées.
Cas de l'hémisphère céleste occidental fig 7:
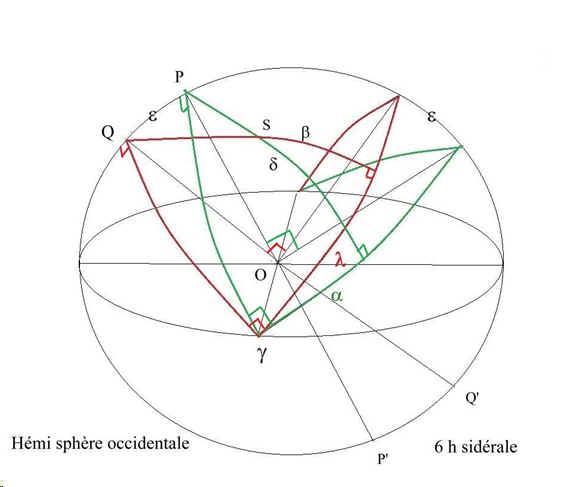
fig 7 l
Nous représentons cette sphère à 6h sidérale le point g étant au couchant sur l'horizon au point cardinal Ouest. L'écliptique et l'équateur ont leur angle de plus
grande pente e sur le méridien du lieu. L'astre S est à l'Ouest.
Le pôle de l'écliptique et celui de l'équateur sont également dans le méridien faisant un angle entre eux égal à e. Soit un astre S.
On fait passer par celui-ci un cercle horaire faisant sur l'équateur un angle a égal à l'ascension droite de l'astre S.
On fait également passer par S un grand cercle ayant pour diamètre les pôles de l'écliptique QQ'.
Ce grand cercle perpendiculaire à l'écliptique fait avec le grand cercle origine Qg un angle correspondant à la longitude éclipique l.
La déclinaison de S par rapport à l'équateur est d et la latitude écliptique de S par rapport à l'écliptique est ß.
Dans le triangle sphérique QPS on a QP = e, QS = p /2 – ß, PS = p /2 – d, QPS = p /2 + a et
PQS = p /2 – l
Cas de l'hémisphère céleste oriental (fig 8):
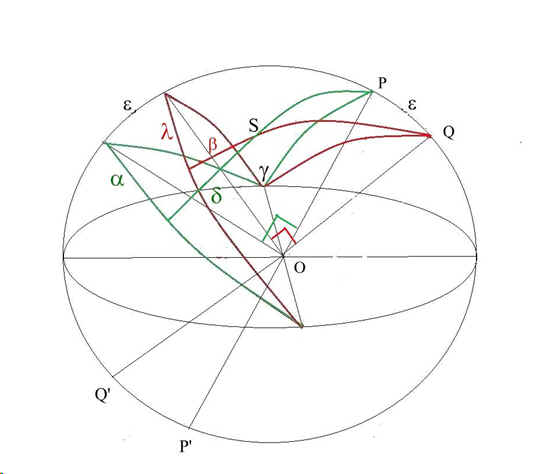
fig 8
On conserve la même configuration: 6 h sidérale point g au couchant au point cardinal Ouest mais l'astre S est à l'Est.
On retrouve les mêmes valeurs pour les côtés mais ici on a QPS = p – (a – p /2) = 3 p /2 – a
et PQS = l – p /2
Comme ci-dessus pour les coordonnées écliptiques les transformations trigonométriques donnent finalement les mêmes formules pour les deux cas.
En prenant pour initiaux le côté PS et l'angle QPS on aboutit au système d'équations permettant de passer des coordonnées équatoriales aux coordonnées écliptiques:
sin ß = cos e sin d – sin e cos d sin a
cos ß cos l = cos d cos a
cos ß sin l = sin e sin d + cos e cos d sin a
En prenant pour initiaux le côté PS et l'angle PQS on aboutit au système d'équations permettant de passer des coordonnées écliptiques aux coordonnées équatoriales:
sin d = cos e sin ß + sin e cos ß sin l
cos d cos a = cos ß cos l
cos d sin a = - sin e sin ß + cos e cos ß sin l
Ces derniers types de coordonnées n'ont que peu d'intérêts en gnomonique. Elles peuvent néanmoins servir dans quelques cas particuliers comme par exemple
la construction de cadrans à heures sidérales et la position du nonagésime sur le cadran solaire.
Cela sera traité dans un prochain paragraphe. Elles sont par contre utilisées en astronomie pour la détermination des mouvements planétaires.
Jean Pakhomoff 18 4 2014