Droite de Simson et cercles
attachés au triangle quelconque
- La droite de Simson

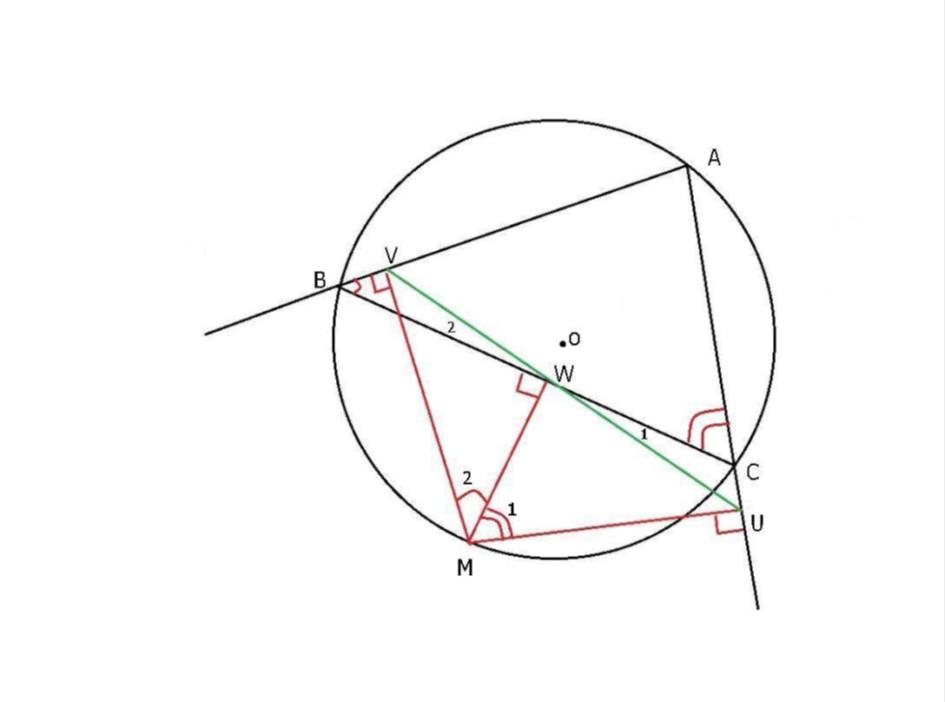
Soit un triangle quelconque ABC inscrit dans un cercle de centre O.
Soit M un point de ce cercle. On projette M orthogonalement sur les 3 côtés du triangle.
On se propose de montrer que les 3 points d'intersection V, W et U entre les projections et les côtés se trouvent sur une droite VWU.
De par leurs côtés perpendiculaires 2 à 2 les angles M2 et ABC sont égaux de même que les angles M1 et BCA.
Dans BVW on a W2 = pi – (B + BVW) = pi -M2 -BVW
Dans WCU on a W1 = pi – (WUC + WCU) WCU = pi – M1
et WUC = pi – (AVU + BAC) ; BAC = pi - (M1 + M2) et AVU = pi – BVW
D'où WUC = pi – (pi – BVW + pi – (M1 + M2)) = BVW – pi + M1 + M2
et W1 = pi – (BVW – pi + M1 + M2 + pi – M1) = pi – BVW + pi – M1 – M2 – pi + M1
W1 = pi –BVW – M2 = W2
Les angles W1 et W2 sont égaux et deux de leurs côtés étant sur une même droite BC côté du triangle ABC, les deux autres côtés sont également sur la droite VWU.
Ainsi les points de projection du point M du cercle circoncrit au triangle ABC sur les côtés de ABC se trouvent sur une droite.
- Cercles inscrit et circonscrit au triangle
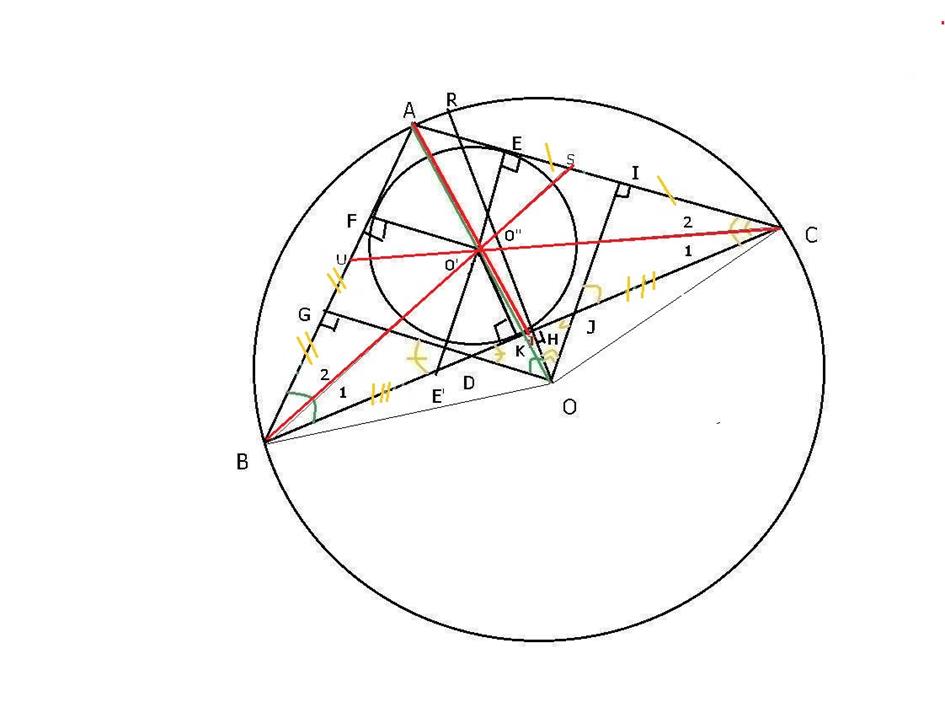
fig 1
(Les imprécisions graphiques de cette figure faîte à "souris levée" ne diminuent en rien la rigueur du raisonnement)
Soit le triangle quelconque ABC et ses trois bissectrices AT, CU et BS. On sait qu'elles se croisent en O' centre du cercle inscrit O' où O'K = O'F = O'E sont les rayons r
de ce cercle perpendiculaires aux 3 côtés.
On trace également le cercle circonscrit de centre O et le rayon OR = R médiatrice de BC coupant BC en H. OI et OG les deux autres médiatrices.
Le rayon OA coupe BC en Z, OO' coupe BC en W et la bissectrice AO' coupe BC en T (voir fig 2)
- Calcul de R
Par rapport à l'arc BC, BOC est l'angle au centre double de l'angle au sommet BAC.
Dans le triangle isocèle BOC on a COH = COB / 2 = 2 BAC / 2 = BAC et
HC = BC / 2 = OC sin COH = R sin COH d'où R = BC / 2 sin A
- Calcul de r
BO'C => sin B1 / O'C = sin BO'C / BC BO'C = pi – (B1 + C1) =>
O'C = sin B1 . BC / (sin B1 + C1)
EO'C=> O'C sin C2 = O'C sin C1 = O'E = r et
r = sin B1. BC sin C1 / sin (B1 + C1) = sin B1. BC sin C1 / (sin B1 cos C1 + sin C1 cos B1)
En divisant haut et bas par sinB1 sin C1 on obtient
r = BC / (1 / tg C1 + 1 / tg B1) = BC / (1 / tg (C/2) + 1 / tg (B/2))
- Rapport des rayons
R / r = (BC / 2 sin A) / (BC / (1 / tg C1 + 1 / tg B1)) =
(1 / tg C1 + 1 / tg B1) / 2 sin A et
R / r = (1 / tg (C/2) + 1 / tg (B/2)) / 2 sin A
- Angle formé entre la droite OO' reliant les cercle inscrit et circonscrit avec le côté BC.
Pour cela agrandissons la partie O'KOH de la figure 1 pour rendre la figure plus lisible:
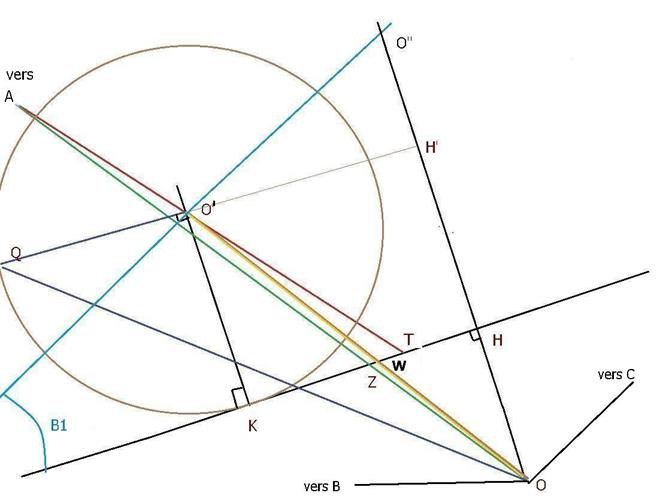
fig 2
On retrouve la bissectrice AT coupant BC en T, le rayon AO du cercle circonscrit.
O'K = r = H'H = est connu. La figure 1 nous permet d'écrire OH = OC cos HOC
HOC = BOC / 2 = 2 A / 2 = A et OH = R cos A d'où H'O = r + R cos A
O'K / BK = r / BK = tg B1 et BK = r / tg B1 BH = BC / 2
KH = O'H' = BH – BK = BC / 2 – r / tg B1
tg H'O'O = OH' / O'H'= (r + R cos A) / (BC / 2 – r / tg B1)
d'où H'O'O = O'WB (alternes internes) angle fait entre la droite O'O joignant les centres des cercle inscrit et circonscrit et
le côté BC opposé à l'angle inscrit A. La connaissance de la valeur de cet angle permettra la comparaison avec l'angle NEH fait entre la droite d'Euler et le côté BC.
la distance entre O et O' est alors OO' sin H'O'O = OH'
OO' = OH' / sin H'O'O = (r + R cos A) / sin H'O'O
En comparant les valeurs de OO' et de tg H'O'O on peut écrire que
r + R cos A = OO' sin H'O'O = tg H'O'O (BC / 2 – r / tg B1) (B1 = B/2)
et OO' = (BC / 2 – r / tg (B/2)) / cos H'O'O
Jean Pakhomoff 13 10 2014 __________
__
- La droite et le cercle des 9 points d'Euler_____
Retour à "Mes travaux personnels"