
De quelques positions remarquables
des aiguilles d'une horloge
Jean Pakhomoff le 4 6 2014
Nous nous proposons de rechercher les heures pour lesquelles les aiguilles d'une horloge se trouvent dans des positions particulières.
Nous choisissons les 4 cas de figures les plus représentatifs.
1) Aiguilles confondues
2) Aiguilles opposées
3) Aiguilles perpendiculaires
4) Aiguilles symétriques par rapport à la ligne 12h - 6h

Horloge Atmos
Généralités:
On remarquera tout d'abord que la petite aiguille fait un tour de cadran en 12 heures ou 720 minutes.
L'arc parcouru par unité de temps est donc égal à 360°/720 = 2 p radians / 720 = p radians / 360.
Après un temps t l'arc MP parcouru par la petite aiguille est donc égal à p t / 360 radians.
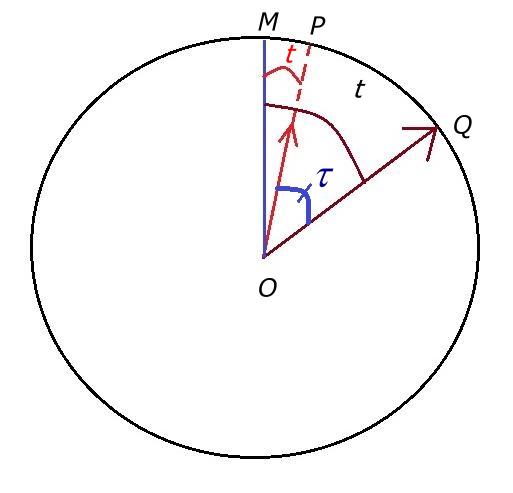
La grande aiguille fait un tour de cadran en 1 heure ou 60'.
L'arc parcouru par unité de temps est donc de 360°/ 60 ou 2 p radians / 60 = p / 30 radians et au bout du même temps t
l'arc MQ parcouru par la grande aiguille est égal à p t / 30 radians. On remarque alors que l'angle POQ = t
différence entre MOQ et MOP est égal à p t / 30 – p t / 360 = 11 p t / 360 radians.
Cette valeur sera utilisée pour la recherche des heures considérées.
Nous la comparerons aux valeurs angulaires faites par les aiguilles dans la position considérée.
Horloge astrolabe Hour Lavigne
1) Aiguilles confondues.
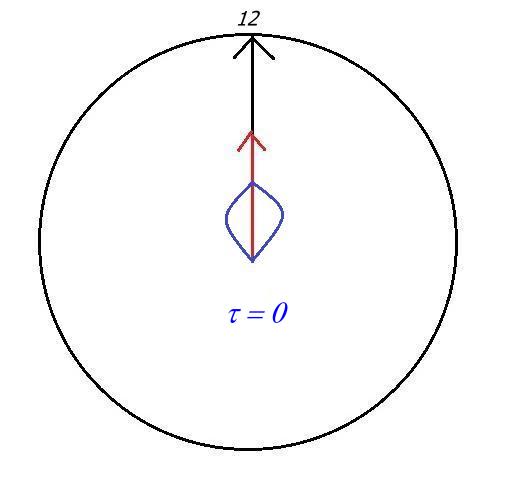
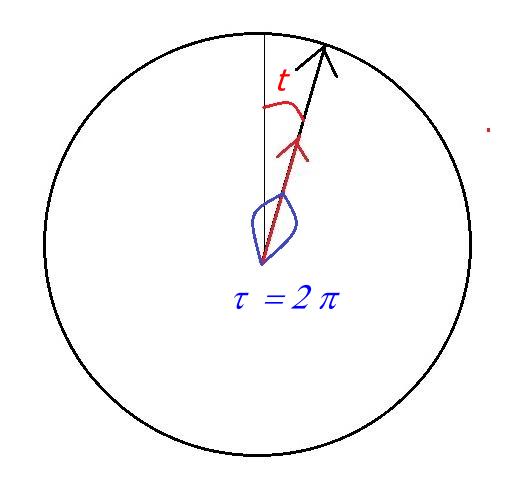
A t = 0 les deux aiguilles sont confondues et t = 0 . Lorsque à t les aiguilles sont de nouveau confondues t = 2 p
Nous avons vu ci-dessus qu'à l'instant t, t = 11 p p t / 360
d'où 11 p t / 360 = 2 p et t = 720 / 11 = 65,4545' = 1h 5' 27''
Le premier alignement se produit à 1h 5' 27''.
Lorsque t aura de nouveau augmenté de 2 p surviendra le deuxième alignement. Celui-ci se fera à
11 p t / 360 = 2 p + 2 p et t = 4 X 360 / 11 = 2 X 720 / 11 = 2h 10' 54''
Le troisième alignement se fera de la même façon et l'on trouve
t = 6 X 360 / 11 = 3 X 720 / 11 = 3h 16' 21''
Les alignements se font donc toutes les 1h 5' 27'' et l'on peut écrire la formule générale:
t n = N X 720 / 11 ainsi le 9è alignement surviendra à
t9 = 9 X 720 / 11 = 9h 49' 5'' et le 11è à 720' = 12h : la petite aiguille a fait un tour complet.
2) Aiguilles opposées.
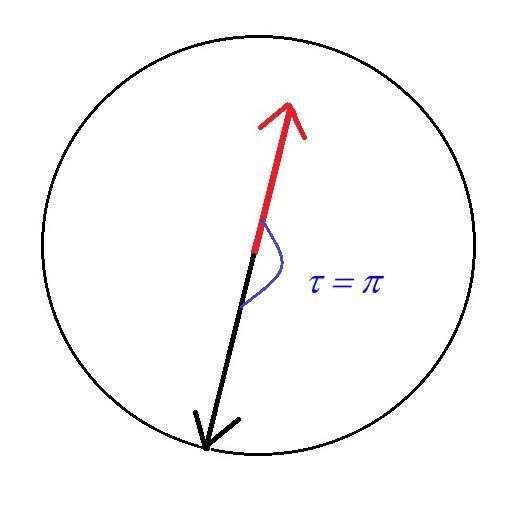
Lorsque cette condition est réalisée t = p
Donc t = 11 p t / 360 = p => t = 360 / 11 = 32' 43'' et la première opposition a lieu à 12h 32' 43''
La deuxième a lieu lorsque t a augmenté de 2 p:
t = 11 pi p / 360 = p + 2 p et t = 3 X 360 / 11 = 1h 38' 10''
La troisième à 11 p / 360 = p + 2 p + 2 p => t = 5 X 360 / 11 = 2h 43' 38''
On tire la formule générale tn = (2 N – 1 ) 360 / 11
Ainsi la 9 è opposition a lieu à (2 X 9 – 1) 360 /11 = 9h 16' 21'''
et la 12è à (2 X 12 – 1) 360 / 11 = 12h 32' 43'' (même heure que la première) etc…
Horloge Regain
3) Aiguilles perpendiculaires.
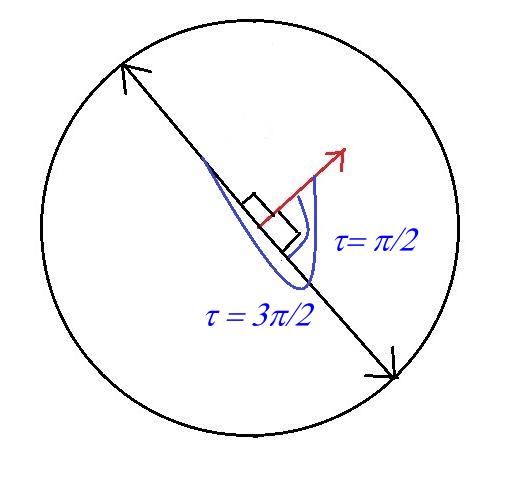
ici t est successivement égal à p / 2 et 3 p / 2. L'incrémentation est égale à p.
La première perpendicularité se fera quand t = p / 2 = 11 p t / 360 et t = 180 / 11
Ce qui correspond à 12h 16' 21''
Pour la deuxième on aura p / 2 + p = 11 p t / 360 et t = 3 X 180 /11 (12h 49'5'')
Pour la troisième on a p / 2 + p + p = 11 p t / 360 et t = 5 X 180 / 11 (1h 21' 49'')
On tire la formule générale tn = (2 N – 1) 180 / 11
Ainsi la 8è perpendicularité aura lieu à 4h 38' 10''
et la 23è à 12h 16' 21''. On est revenu à la première position.
4) Aiguilles symétriques par rapport à la ligne XII-VI.

Ici t = 2 p – 2 arcs t On a vu au début que la valeur de l'arc t en radians était de
2 p t / 720 = p t / 360
On a donc 2 p – 2 p t / 360 = 11 p t / 360 d'où l'on tire t =720 / 13 = 55,3846'
ce qui correspond à 12h 55' 23''. (heure de la première symétrie)
En augmentant t de 2 p on aura t = p p – 2 arcs t + 2 p <=> 2 p – 2 arcs t
On se retrouve dans les conditions de la symétrie et on peut écrire
2 p + 2 p – 2 p t / 360 = 11 p t / 360 en simplifiant par p il vient:
4 – 2 t/ 360 = 11 t / 360 et t = 1440 / 13 = 2 X 720 / 13 <=> 110,7692' <=> 1h 50' 46'' (2è symétrie)
Pour la 3è symétrie on incrémente de 2 p et on trouve
t = 2160 / 13 = 3 X 720 / 13 <=> 166,1538' <=> 2h 46' 9''
On peut écrire que la Nè symétrie est donnée par tn = N X 720 / 13
Ainsi la 10è se fait à 720 / 13 <=> 9h 13' 50''
et la 13é se fait à 13 X 720 / 13 <=> 12 heures (aiguilles confondues sur la ligne XII-VI)
Reour à "Mes travaux personnels"
Horloge Regain