Domifications de Régiomontanus

et de Placidus

Jean Pakhomoff

_ Nous étudions dans ce travail sous leur aspect géométrique les deux domifications les plus utilisées en astrologie.

_ L'une dîte de Régiomontanus a déjà fait l'objet d'une étude publiée sur ce site vers 1996.

_Nous l'avons remaniée et adaptée en la complétant avec la domification dîte de Placidus.

__ Il existe un grand nombre d'autres méthodes de divisions de la sphère céleste. Nous nous limiterons à celles-ci car ce sont les plus classiques.

____La valeur prédictive que l'astrologie attribue à chacune des maisons célestes ne sera pas évoquée.

____Seule la valeur numérique de l'arc zodiacal contenu dans chaque maison aura retenu notre attention.

Le calcul de l'ascendant est commun aux deux domifications. Nous commencerons donc par celui-ci.

Envisageons d'abord le cas de l’hémisphère nord et nous verrons ensuite comment procéder pour domifier l’hémisphère sud.

Mettons gamma (g) point d'intersection de l'équateur céleste et de l'écliptique (zodiaque) au point Est et

faisons le tourner de 2 pi dans le sens rétrograde (horaire). Lorsque g est au point Est il est 18 heures sidérales.

g au méridien supérieur <=> 0 h sidérale, g au point ouest <=> 6 h sidérale et g au méridien inférieur <=> 12 h sidérale.

Dans l'hémisphère nord l’écliptique tourne depuis le point g au cardinal Est et son lever coupe l’horizon au nord est

de l’équateur céleste, ce jusqu’à ce que g atteigne le cardinal Ouest à 6 h sidérale après passage à 0h (méridien).

Ensuite g passe sous l’horizon et de 6 h à 18 h sidérales, après passage à 12 h au méridien inférieur,

le lever de l’écliptique se fait au sud est de l’équateur céleste.

Précisons ici que le point gamma de même que les étoiles tournent sur la sphère locale dans le sens rétrograde d'est en ouest.

Le soleil vu de la terre "se déplace" par contre dans le sens direct (anti-horaire) dans le zodiaque.

Le point gamma se déplace également dans le zodiaque dans le sens rétrograde de par le mouvement de précession des équinoxes.

Il fait un tour de zodiaque complet en un peu plus de 25000 ans. En conséquence de nos jours le printemps ne se fait plus à l'entrée en Bélier mais vers la sortie des Poissons. Et dans quelques siècles il se fera à l'entrée en Verseau

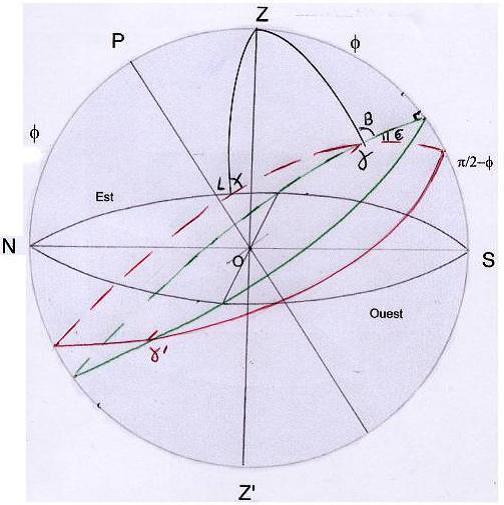
1) entre 18h et 0 h sidérales (figure 1). soit L le lever de l’écliptique, N le nord, S le sud, Z le zénith.

fig 1

Dans la suite de cet exposé nous appellerons Zg (Z gamma): Z

Descendons un vertical depuis Z sur g. Soit B l’angle ZgEq dans le triangle sphérique ZgEq.

on a sin B / sin f = sin 90 / sin Zg   d’où   sin B = sin f / sin Zg (1)

Zg est la hauteur zénithale de g, donnée par la formule de la hauteur lorsque d = 0 (cas de g) :

cos Zg = cos f cos t (2) t étant l’angle horaire de g ici 270 < g < 360

Lorsque t = 3 pi/2 Z = pi/2 et B = f

si t = 2 pi = 0 Z = f , sin B = 1 et B = pi/2

donc B croît de f à pi/2 quand t croît de 3 pi/2 à 2 pi

Faisons passer un vertical par L point commun à l’horizon et à l’écliptique.

Le triangle ZLg permet d’écrire sin (pi-B-ep) / sin (pi/2) = sin (B+ep) / 1 = sin L / sin Z

d’où sin L = sin Z sin (B+ep) (3)

de même cos Z = cos Lg cos pi/2 + sin Lg sin pi/2 cos L d’où sin Lg = cos Z / cos L (4)

Dans l’hémisphère nord, à un certain moment, l’arc Lg va dépasser 90° .

Le lever se faisant au nord, lorsque g approche du méridien l’arc Lg est nécessairement plus grand

que l’arc d’équateur céleste correpondant.

(3) ne rend pas directement la valeur de Lg quand Lg>pi/2. En effet sin Lg a même valeur que Lg soit>ou< pi/2.

Lorsque Lg = pi/2 on a cos Z = cos L et L = Z.

On peut alors écrire (3) sin L = sin L sin (B+ep) d’où sin (B+ep) = 1 et B+ep = pi/2

Comme nous l’avons vu, dans le cas de figure où 270<t<360 B croît de f à pi/2.

On en déduit que si B+ep<pi/2, Lg<pi/2 et si B+ep>pi/2 alors Lg>pi/2.

Dans le programme informatique gwbasic on précisera donc : si B+ep<pi/2 alors Lg=Lg

si B+ep>pi/2 alors lg=pi-Lg

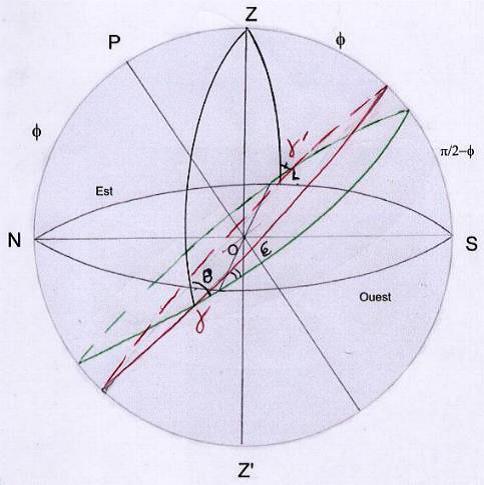
2) Entre 0 heure et 6 heures sidérales. (figure 2)

fig 2

d’aprés (2) à 0 h t = 0 ==> Z = f ; à 6 h t = pi/2 ==> Z = pi/2

d’aprés (1) si Z = f ==> B = pi/2 ; si Z = pi/2 ==> B = f ; B décroît donc de pi/2 à f quand t croît de 0 à pi/2

Zlg permet d’écrire sin (B-ep)/sin pi/2 = sin L/sin Z ===> sin L = sin Z sin (B-ep)

On a de même cos Z = cos Lg cos pi/2 + sin Lg sin pi/2 cos l et on retrouve (4) sinLg = cosZ / cos L

Ici Lg sera toujours >pi/2 et au maximum égal à pi à 6 h sidérales.

Donc on posera dans le programme Lg = pi - Lg (l’ordinateur donnant la valeur de l’angle le plus petit).

(par exemple sin 120 <=> arcsinus 120 = 60 d’où 120 = 180 - 60)

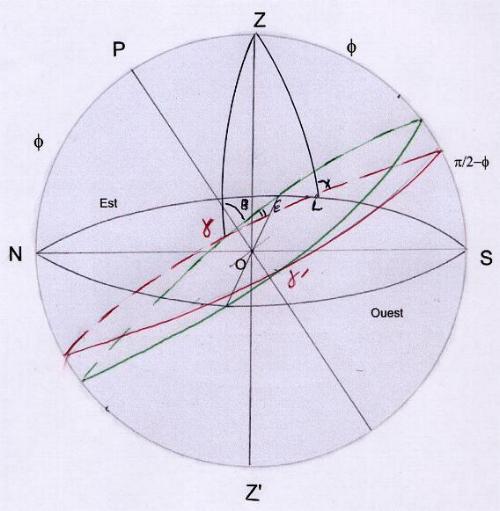
3) Entre 6 h et 12 h sidérales. (figure 3) Ici g passe sous l’horizon.

fig 3

___Pour t = 6 h cos t = 0 et Z = pi/2 ; pour t = pi (12 h sidérales)

___cos t = -1 et cos Z = - cos f = cos (pi - f)

___donc quand t croît de 6 à 12 h , Z croît de pi/2 à pi - f.

___d’aprés (1) pour t = pi/2 , Z = pi/2 et B = f

___pour t = pi , Z = pi - f et sin B = 1 d’où B = pi/2 : lorsque t croît de pi/2 à pi, B croît de f à pi/2.

___sin (B-ep) / sin pi/2 = sin L / sin Z ==> sin L = sin Z sin (B-ep) on retrouve de même (4)

___Ici lorsque t = pi Lg est < 3pi/2 . En effet le lever de l’écliptique se fait au sud de l’équateur terrestre et l’arc d’écliptique

___entre l’horizon est et le méridien est nécessairement infèrieur à l’arc d’équateur céleste correpondant égal à pi/2.

___donc pi+arc<pi/2 <=> arc < 3pi/2. Lg sera donc compris entre pi et 3pi/2.

___L’ordinateur donnera l’arc -Lg correspondant : on posera alors dans le programme Lg = pi - Lg (puisque Lg a une valeur négative).

___Exemple: sin 240 <=> arc sinus 240 = - 60 et 240 = 180 -(-60) )

___Entre 12 et 18 h sidérales. (figure 4).

fig 4

(2) montre qu’à 18 h Z = pi/2. A 12 h Z = pi-f. Donc lorsque t croît de pi à 3pi/2 Z décroît de pi-f à pi/2.

(1) montre que pour t = 3pi/2 , Z étant égal à pi/2 => B = f. Si t = pi Z = pi-f et sin B = 1 <=> B = pi/2.

Donc quand t croît de pi à 3pi/2, B décroît de pi/2 à f.

On a de même sin (B+ep) / sin pi/2 = sin (pi-L) / sin Z d’où sin L = sin Z sin (B+ep) (3’)

A un certain moment, entre 12 et 18 h sidérales, Lg va dépasser la valeur 3pi/2.

si Lg < 3pi/2 on a vu qu’il fallait prendre Lg = pi - Lg (ici Lg est <0).

si Lg > 3pi/2 l’ordinateur donne la valeur angulaire minimale (par exemple sin 300° et arc sin 300° = -60°)

donc il nous faudra écrire dans le programme : Lg = 2pi+Lg (puisque Lg est <0)

Lorsque Lg = 3pi/2 on a sin Lg = cos Z / cos L = -1 d’où Z = pi-L et (3’) permet d’écrire:

sin L = sin (pi-L) sin (B+ep) ==> sin (B+ep) = 1 et B+ep = pi/2

On a vu que dans ce cas B décroît de pi/2 à f. On en déduit que si B+ep > pi/2 alors Lg < 3pi/2 et on emploiera alors Lg = pi-Lg.

si B+ep < pi/2 alors Lg > 3pi/2 et on emploiera Lg = 2pi+Lg.

Arrivé à ce stade de notre étude nous avons donc le moyen, à partir d’un temps sidéral donné, de connaître

la longitude de l’écliptique à son lever et en ajoutant ou retranchant pi la valeur du descendant.

En soustrayant pi/2 à la valeur de l’ascendant on obtient le nonagésime : milieu de l’arc d’écliptique au-dessus de l’horizon qui ,

sauf à 18h et 6h sidérales est toujours à l’est ou à l’ouest du méridien (qui lui donne le milieu du ciel).

Avant d'en terminer avec la détermination de l’ascendant étudions les 4 cas particuliers que sont :

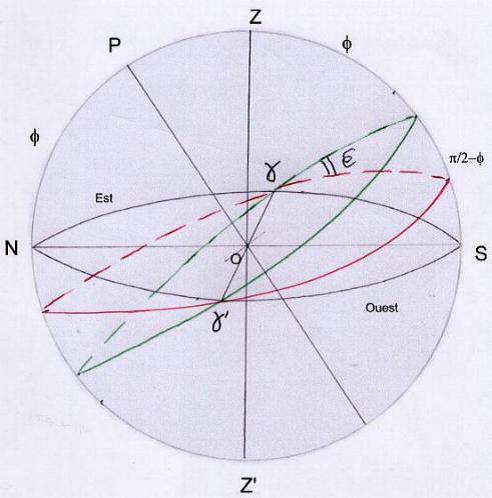
a) cas de 18 h sidérales: (figure 5)

fig 5

Gamma est au point est. la longitude du lever de l’écliptique est donc 0. C’est le lever du signe (et non de la constellation)

du bélier et le coucher de la balance. Le capricorne (270°) est le nonagésime au milieu du ciel. Le cancer (90°) représente le fond du ciel.

b) cas de 0 h sidérale: (figure 6)

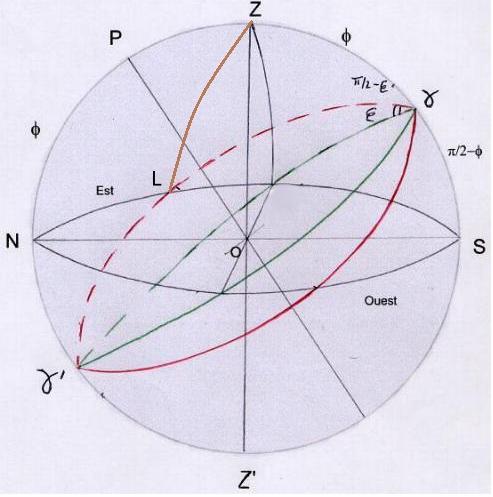fig 6

Gamma est au méridien. ZLg permet d’écrire sin L / sin f = sin (pi/2-ep) / sin (pi/2) ==> sin L = sin f cos ep

cos f = cos pi/2 cos Lg + sin pi/2 sin Lg cos l et sin Lg = cos f / cos L

ici on l’a vu Lg > pi/2 : on prendra donc Lg = pi-Lg

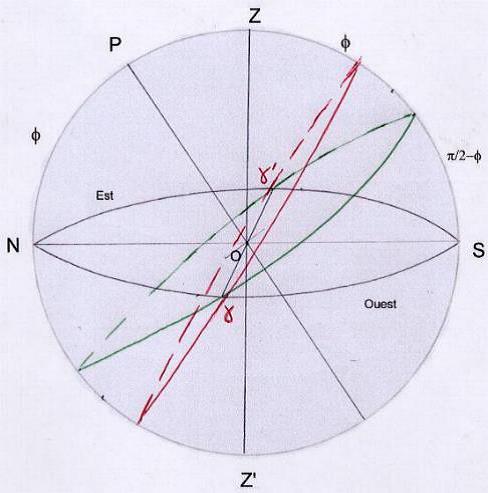
c) cas de 6 h sidérales: (figure 7)

fig 7

Gamma’ est au point est. La balance (180°) se lève et le bélier se couche.

Le cancer est le nonagésime au milieu du ciel et le capricorne est le fond du ciel.

d) cas de 12 h sidérales: (figure 8)

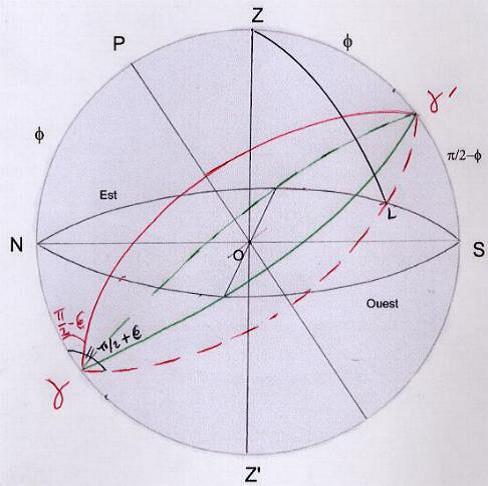
fig 8

Gamma est à l’anté-méridien et gamma’ passe au milieu du ciel

on a Zg = pi/2+pi/2-f = pi-f. ZLg ==> sin L / sin (pi-f) = sin(pi/2-ep) / sin pi/2 et

sin L = sin f cos ep; de même cos (pi-f) = cos pi/2 cos Lg + sin pi/2 sin Lg cos L et sin Lg

= - cos f / cos L. Ici on a vu que Lg est compris entre pi et 3pi/2. On prendra alors Lg = pi - Lg

(car Lg est donné <0 , f et L étant < pi/2)

Domification de Régiomontanus.

fig 9

Dans la domification de Régiomontanus les maisons sont des secteurs de sphère céleste limités par des grands cercles

passant par les point Nord et Sud de l’horizon et coupant l’équateur céleste de 30 en 30° à partir du point Est de l’horizon dans le sens rétrograde.

fig 9'

a) Détermination de l’angle dièdre M fait entre une cuspide quelconque et l'horizon est (cuspide I):

par exemple angle entre la cuspide I ou pointe de la maison I et la cuspide XII (maison XII).

Les maisons diurnes commencent à l’ascendant par la pointe de la maison 1 (qui elle est le grand cercle de l’horizon côté Est)

. fig 10

Ensuite d’Est en Ouest on trouve la maison 12 , 11, 10 (la pointe de 10 étant le méridien ou milieu du ciel), puis 9, 8, 7

(la pointe de 7 étant le grand cercle de l’horizon côté ouest ou descendant), puis les maisons nocturnes 6, 5, 4

(la pointe de 4 est l’anté-méridien ou fond du ciel), et 3, 2, 1.

Nous appellerons L (figures 11 et suivantes) le point de lever de l’écliptique, T le point Est de l’horizon, N le point Nord,

D le point Sud, E l’intersection d’un cercle de domification avec l’équateur et S l’intersection d’un tel cercle avec l’écliptique.

Nous appellerons M l’angle de secteur des pointes des maisons avec l’horizon (angle variant de 30° pour la maison 12 à 360° pour la maison 1).

TE sera l’angle correpondant sur l’équateur céleste. Par exemple pour la maison 12 , TE = 30° et pour la maison 3, TE = 300°.

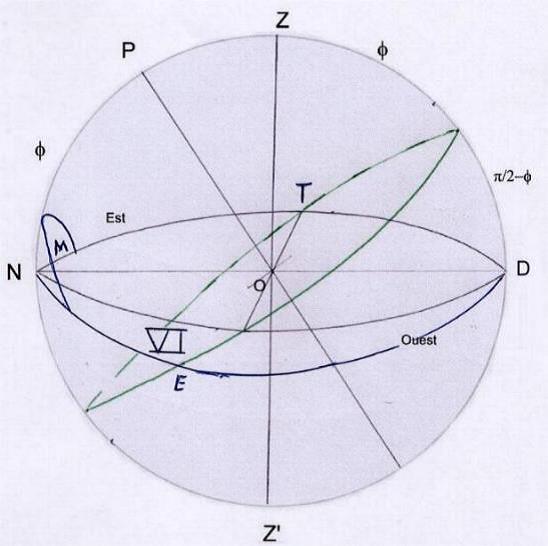fig 11

___Le triangle sphérique NTE permet d’écrire

___cos NE = cos NT cos TE + sin NT sin TE cos (pi/2 + f) d’où cos NE = -sin TE sin f (NT = pi/2)

___cos TE = cos NE cos NT + sin NE sin NT cos M et

___cos M = cos TE / sin NE

___L’ordinateur donne les angles à partir de leurs arc tangentes. Il est donc nécessaire d’utiliser les formules de tranformation citées c-dessus.

___Pour les maisons 12, 11 et 10 TE < pi/2, cos NE<0 =>NE > pi/2 , cos M > 0 et M < pi/2

___Donc l’ordinateur fournira M = M (transformation de l’arc cosinus en arc tangente).

___Pour les maisons 9, 8 et 7 pi/2< TE < pi. Dans ce cas cos NE < 0 <=> NE > pi/2 <=> sin NE > 0

___cos TE < 0 => cos M < 0 On rajoutera donc pi à la valeur fournie par l’ordinateur

___(exemple cos 2pi/3= x => l’arc tangente de transformation donne pour x un angle de - pi/3) . On écrira dans le programme M = M + pi.

___Pour les maisons 6, 5 et 4 on a pi< TE < 3pi/2 on a sin TE < 0 et cos TE < 0 => cos NE > 0

___et NE < pi/2 => sin NE > 0 => cos M < 0. Ici il nous faudra prendre M = pi - M (M étant < 0)

___Pour les maisons 3, 2, 1 3pi/2<TE<2pi => sin TE < 0 et cos NE > 0 => NE < pi/2 et sin NE > 0

___cos TE > 0 => cos M > 0. Il nous faudra prendre ici M = 2pi - M.

___Notons que si TE = pi/2 cos M = 0 et M = pi/2

___si TE = pi M = pi , TE = 3pi/2 => M = 3pi/2 et TE = 2pi => M = 0 ou 2pi

___b) Position de gamma par rapport à l’horizon.

___1) gamma sur l’horizon (fig 12)

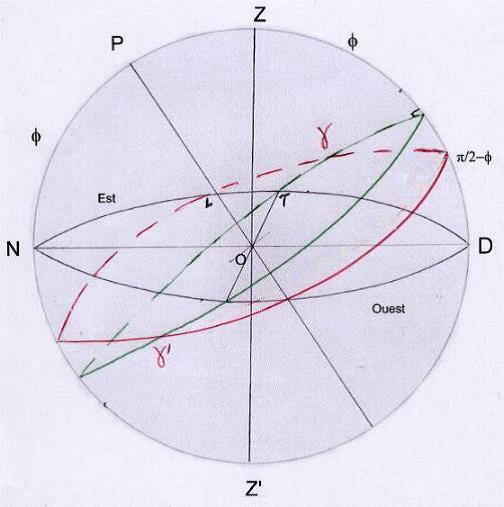fig 12

On a vu qu’ici l’écliptique au lever coupait l’horizon dans sa partie nord. Le triangle LTg permet d’écrire

sin (pi/2 + f) / sin Lg = sin ep / sin LT d’où sin LT = sin ep sin Lg / cos f

ep et f sont connus et le début de cette étude nous permet de calculer Lg.

On considérera la quantité LN = pi/2 - LT (quand g passe au méridien Lg > gT).

2) gamma sous l’horizon (fig 13).

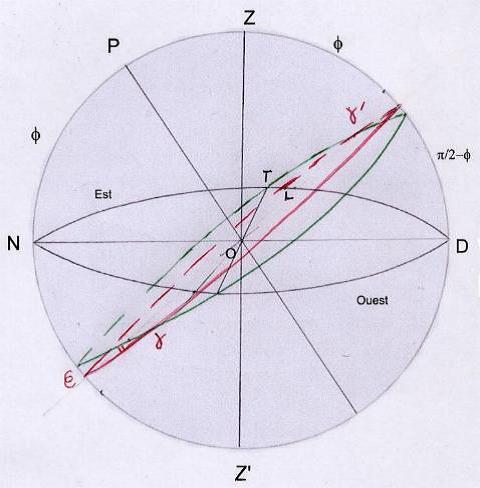fig 13

Dans l’hémisphère nord l’écliptique coupe dans ce cas l’horizon vers le sud. De LTg on tire

sin ep / sin Lt = sin (pi/2 + f) / sin (2pi - Lg) et sin LT = - sin ep sin Lg / cos f

On considérera la quantité LN = pi/2 + LT ( quand gamma’ passe au méridien Lg’<Tg’ et par suite Lg’<pi/2).

Cette grandeur LT rend compte de la limite des domifications Régiomontanus et Placidus.

En effet la valeur maximale de LT est égale à pi / 2 et sin LT = 1. A ce moment là la latitude est égale au complément

de la déclinaison du solstice d'été et sin ep / cos f = 1. sin Lg est égal à 1 et Lg à pi / 2. L'arc diurne du Cancer tangente

l'horizon du cercle arctique alors que l'arc diurne du Capricorne tangente l'horizon du cercle antarctique.

Pour des latitudes supérieures on a f > pi / 2 – ep

cos (pi / 2 – ep) est alors < cos f et sin LT est > 1 ce qui est impossible.

Il n'est donc pas possible de domifier les zones polaires par les méthodes Régiomontanus et Placidus.

Les habitants de ces contrées ne sont cependant pas privés de leur horoscope car d'autres méthodes de domification existent.

c) Calcul de la grandeur d’arc d’écliptique compris dans le secteur d’une maison. (figure 14)

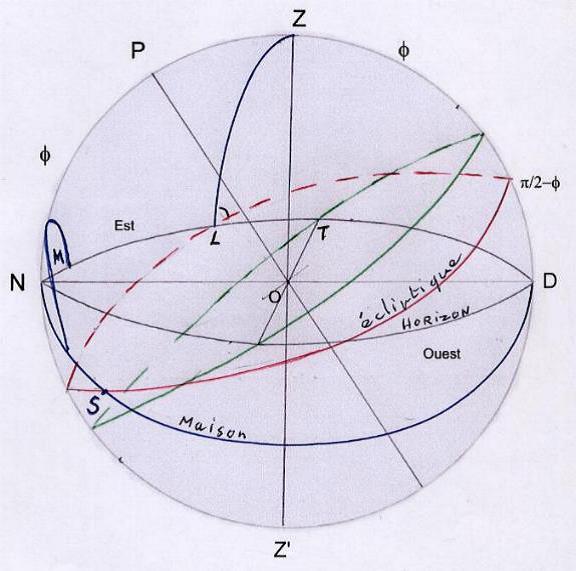fig 14

On connaît L, LT, LN et M. Considérons le triangle sphérique LSN.

On a sin NS / sin (pi/2 + L) = sin sin LS / sin M d’où sin NS = sin LS cos L / sin M

cos LS = cos NS cos NL + sin NS sin NL cos M et

cos NS = (cos LS - sin NS sin NL cos M) / cos NL en remplaçant sin NS par sa valeur on obtient

cos NS = [cos LS - (sin LS cos L / sin M) sin NL cos M ] / cos NL

De même cos NS = cos LS cos NL + sin LS sin NL cos (pi/2 +L)

= cos LS cos NL - sin LS sin NL sin L

et en comparant les 2 valeurs de cos NS il vient

cos LS - (sin LS cos Lsin M) sin NL cos M = cos² NL cos LS - sin LS sin NL cos NL sin L

divisons par cos LS

1- (tg LS cos L / sin M) sin NL cos M = cos² NL - tg LS sin NL cos NLsin L

sin² NL = tg LS cos L sin NL cos M / sin M - tg LS sin NL cos NL sin L

sin NL = tg LS cos L cos M / sin M - tg LS cos NL sin L

= tg LS cos L / tg M - tg LS cos NL sin L

sin NL tg M = tg LS cos L - tg LS cos NL sin L tg M

= tg LS (cos L - cos NL sin l tg M)

tg LS = sin NL tg M / (cos L - cos NL sin L tg M) = sin NL / (cos L/ tg M - cos NL sin L)

tg LS = 1 / (cos L / tg M sin NL - sin L / tg NL)

si M tend vers pi/2 ou 3pi/2 tg M tend vers + ou - l’infini et tg LS tend vers sinNL/-cosNLsinL = -tg NL / sin L

d) Variations de la grandeur LS en fonction des maisons considérées.

On tiendra compte de la période de la tangente dans l’appréciation de LS.

1) Cas des maisons 12, 11, 10 (valeurs de LS (12), LS(11), LS(10) )

tg LS > 0 => LS < pi/2 on prend LS = LS

tg LS < 0 => LS > pi/2 on prend LS = pi + LS

2) Cas des maisons 9, 8 et 7 (LS(9) ...)

Ici LS < ou = pi. Si tg LS >0 (LS < pi/2) on pred LS = LS; si tg LS < 0 (LS > pi/2) on prend LS = pi + LS

3) Cas des maisons 6,5,4,3,2 et 1 (LS(6)...): ici LS > pi peut être > ou < à 3pi/2.

Si tg LS > 0 (LS est compris entre pi et 3pi/2) on prend LS = PI + LS

si tg LS < 0 (LS compris entre 3pi/2 et 2pi on prend LS = 2pi + LS (l’ordinateur fournissant l’arc tangente le plus faible).

Par exemple tangente 300 <=> arc tangente- 60 ou 300. L’ordinateur donne -60 : on rajoutte 360.

Si tangente LS = 0 on prendra LS = 0 pour la pointe de la maison 1 (ascendant) ou LS = pi pour la pointe de la maison 7 (descendant).

La portion d’écliptique liée à chaque maison se trouvera en soustrayant les différentes valeurs de LS calculées pour chaque pointe de maison:

par exemple la portion d’écliptique revenant à la maison XII sera valeur de LS(12) - longitude de l’ascendant (Lg),

la portion revenant à la maison XI sera la différence entre L(11) et L(12) etc...

Nous pourrons donc connaître quelle portion du zodiaque se trouve dans chacune des maisons.

Abordons maintenant la domification de la sphère céleste selon Placidus. Nous verrons ensuite comment domifier l'hémisphère sud.

Domification de Placidus

Domification la plus utilisée par les amateurs d'astrologie car mise en tables et publiée dans le commerce ne nécessitant

de ce fait pratiquement aucun calcul pour la connaisance des cuspides des différentes maisons.

Après de fastidieuses recherches dans la littérature et sur internet nous n'avons trouvé aucune démonstration satisfaisante

concernant le calcul de ces maisons. La méthode elle-même est la plupart du temps exposée de façon très nébuleuse et souvent incorrecte.

Seul le livre de Max Duval "La Domification et les Transits" aux Editions Traditionnelles nous a été d'une certaine utilité car il apporte

des précisions bienvenues et correctes sur le système placidien.

Nous allons montrer dans ce travail comment calculer ces maisons et leurs cuspides.

Max Duval ecrit dans son livre "La Domification et les Transits" aux Editions Traditionnelles à propos de la domification de Placidus:

On va alors considérer que par les points Q et Q1 passe un grand cercle qui recouvre l'arc QQ1 joignant les premiers tiers d'arc

semi-diurne lors des solstices (fig 15).

Il nous faudra alors déterminer l'angle dièdre fait entre ce cercle et l'horizon. Nous appellerons cet angle M par analogie avec

l'angle dièdre des maisons type Régiomontanus.

Ce cercle tel que défini pourra représenter sur la figure 15 la maison XII en domification Placidus.

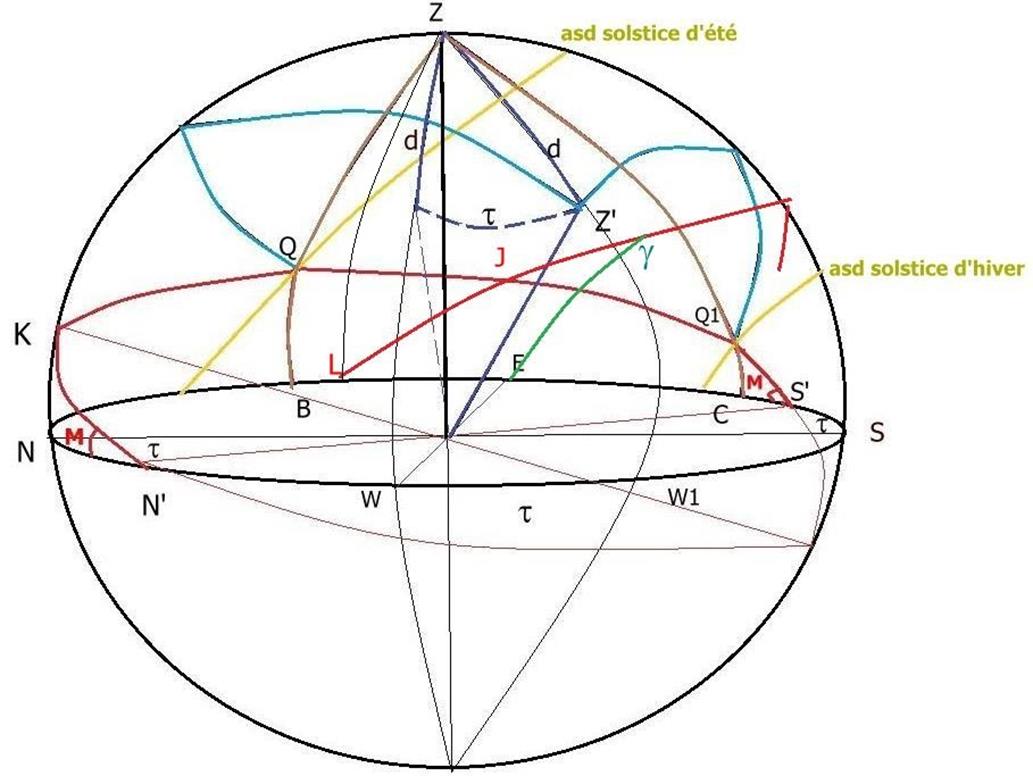fig 15

Appelons ce cercle N'KQQ1S'. Les points Q et Q1 étant à l'est le pôle Z' sur l'horizon de ce cercle sera à l'ouest et le point Q1

étant plus bas (hiver) que le point Q (été) ce pôle sera orienté vers le sud.

Ce pôle se sera donc abaissé d'un angle d par rapport au zénith et aura pivoté d'un angle t par rapport au premier vertical ZW.

(l'axe Nord Sud NS pivote de t et vient en N'S')

Considérons les triangles QBS' et Q1CS' rectangles en B et C (verticaux abaissés de Z sur l'horizon en passant par Q et Q1).

QB est la hauteur hQ de Q et Q1C la hauteur hQ1 de Q1. Ces valeurs sont données par la relation classique du calcul de la hauteur:

sin h = sin f sin d + cos f cos d cos t où h est la hauteur , f la latitude du lieu et d la déclinaison de Q ou de Q1.

On peut écrire les rapports suivants:

tg QB / tg M = sin BS' et tg Q1C / tg M = sin CS' d'où tg M = tg QB / sin BS' = tg Q1C / sin CS'

BS' = BC + CS' et sin BS' = sin BC cos CS' + sin CS' cos BC

tg QB / tg Q1C = (sin BC cos CS' + sin CS' cos BC) / sin CS' = sin BC / tg CS' + cos BC

BC est la différence des azimuts de C et B connus par les relations classiques du calcul de l'azimut:

tg Az = sin t / (sin f cos t – cos f tg d)

On peut alors écrire tg QB / tg Q1C – cos BC = sin BC / tg CS' ou tg hQ / tg hQ1 – cos dA = sin dA / tg CS'

et tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS'

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M

Considérant toujours Q1S'C on peut écrire

cos Q1S' = cos Q1C cos CS' + sin Q1C sin CS' cos pi / 2 d'où cos Q1S' = cos hQ1 cos CS'

cos CS' = cos Q1c cos Q1S' + sin Q1C sin Q1S' cos CQ1S' et

cos CQ1S' = (cos CS' – cos hQ1 cos Q1S') / sin hQ1 sin Q1S' d'où CQ1S'

Soit Z le pôle du grand cercle de l'horizon et Z' le pôle du cercle N'KQQ1S'

Dans le triangle Z'ZQ1 on a ZZ' = d angle entre les deux pôles, ZQ1 = pi / 2 – Q1C = pi/ 2 – hQ1

et Z'Q1 = pi/2 comme vertical du cercle N'KQQ1S'. L'angle Z'Q1Z = pi / 2 – CQ1S' on peut alors écrire que

cos ZZ' = cos d = cos Z'Q1 cos ZQ1 + sin Z'Q1 sin ZQ1 cos Z'Q1Z = sin (pi / 2 – hQ1) cos Z'Q1Z = cos hQ1 sin CQ1S'

on remarquera que d = M comme attendu.

Le pôle Z s'est donc abaissé en Z' de cette valeur d après avoir pivoté de t depuis le premier vertical vers le sud.

Cette valeur t est égale à la valeur 2 pi diminuée de la somme de l'azimut de Q1 et de l'arc CS' que nous avons déterminé plus haut.

t= 2 pi – (AzQ1 + CS')

La pointe de la maison XII est donc donnée par cet angle dièdre M dans le système Placidus.

On trouvera les autres pointes en procédant de la même façon.

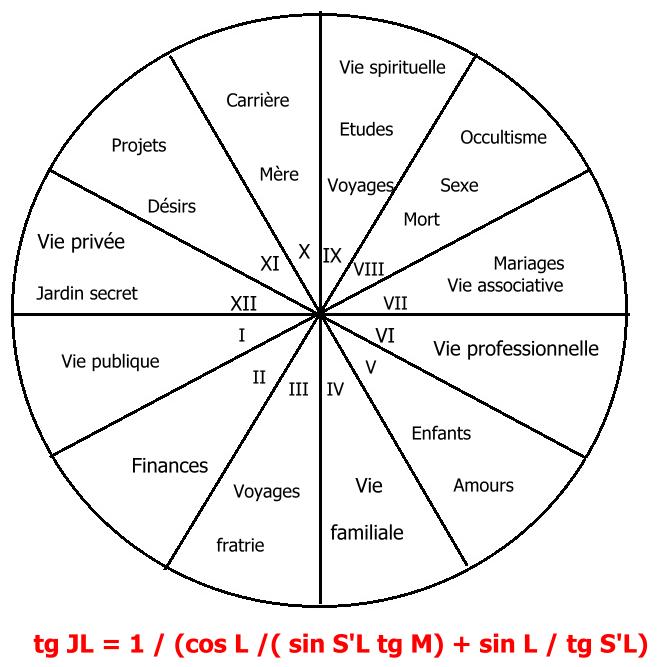
CALCUL de l'arc d'écliptique LJ contenu entre l'horizon et le cercle N'KQQ1S'.

Considérons le triangle sphérique LJS'. on a

sin (pi / 2 – L) / sin S'J = sin M / sin JL d'où sin S'J = cos L sin JL / sin M

cos JL = cos S'J cos S'L + sin S'j sin S'L cos M et

cos S'J = (cos JL – sin S'J sin S'L cos M) / cos S'L

En remplaçant sin S'J par sa valeur on obtient

cos S'J = [cos JL – (cos L sin JL / sin M) sinS'L cos M] / cos S'L

De même cos S'J = cos JL cos S'L + sin S'L sin JL cos (pi / 2 – L) = cos JL cos SL' + sin S'L sin JL sin L

En comparant les deux valeurs de cos S'J il vient

cos S'J = [cos JL – (cos L sin JL / sin M) sin S'L cos M] / cos S'L = cos JL cos S'L + sin S'L sin JL sin L

cos JL – (cos L sin JL / sin M) sin S'L cos M = cos² S'L cos JL + sin S'L sin JL sin L cos S'L

Divisons par cos JL on obtient

1 – (cos L tg JL / sin M) sin S'L cos M = cos² S'L + sin S'L tg JL sin L cos S'L 1 = cos² S'L + sin² S'L

sin² S'L = (cos L tg JL / sin M) sin S'L cos M + sin S'L tg JL sin L cos S'L

sin S'L = cos L tg JL cos M / sin M + tg JL sin L cos S'L = cos L tg JL / tg M + tg JL sin L cos S'L

sin S'L tg M = cos L tg JL + tg JL sin L cos S'L tg M = tg JL (cos L + sin L cos S'L tg M)

tg JL = sin S'L tg M / ((cos L + sin L cos S'L tg M)) = sin S'L / (cos L / tg M + sin L cos S'L) et

tg JL = 1 / (cos L /( sin S'L tg M) + sin L / tg S'L)

Si M tend vers pi/2 tg JL tend vers tg S'L / sin L

L'étude sur la domification de Régiomontanus nous a permis de connaître la valeur LE égale à arc sinus (sin ep sin Lg / cos f)

quand g est au-dessus de l'horizon (temps sidéral compris entre 18h et 6h en passant par 0h) ce qui est notre cas puisque

le temps sidéral est de 22h 13'. Cette valeur de LE est de arc sinus (- sin ep sin Lg / cos f) lorsque gamma est au dessous

de l'horizon (entre 6h et 18h en passant par 12h). Lg est la longitude de l'ascendant.

La valeur de S'L est donc de LE + ES – S'S. ES = pi / 2 (cardinal Est par où passe l'équateur céleste)

S'S = 2 pi – (azimut de Q1 + CS') = tet S'L = LE + pi / 2 – S'SDonnons un exemple chiffré.

Soit donc une naissance ayant lieu le 20 4 2010 à 10 h 0' 0'' en un lieu de latitude 43° nord et de longitude -5° e st.

Les calculs précédents permettent de connaître la longitude de l'ascendant écliptique de l'ascendant qui est égale à

87.297° gémeaux; temps sidéral = 22h 13' = 333.2427° epsilon = 23.4379° en avril 2010; L = 49.1736°

En régiomontanus nous trouvons Cuspide XII = 50.86° (20.86° ou 20° 51' taureau). Les tables placidiennes donnent pour 22 h 13': 16.41° taureau.

Ici on prend t = 2/3 asd (arc semi-diurne) ce qui pour Q correspond à 360 - 75.8968° = 284.1032 et pour Q1 à 360 - 44.1031 = 315.8969

Rappels: - l'arc semi-diurne est égal à arc cos (- tg d tg f)

- lorsque l'angle horaire t varie de 0 à 360° l'azimut Az est donné par la calculatrice sous son expression la plus petite.

Il conviendra donc dans le programme de poser les conditions suivantes: si pi / 2 < ou = t <pi et si Az <0 alors

Az = Az + pi; si pi < ou = t < ou = 3 pi / 2 alors Az = Az + pi et si 3 pi / 2 < t < 2 pi alors Az est <0 et Az = 2 pi + Az

Tous calculs faits on obtient:

hQ = 25.7708 AzQ = 261.1575 hQ1 = 12.1561 AzQ1 = 319.2185 dA = 58.061 longitude Lg de l'ascendant: 87.297°

tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS' = 26.363

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M = 25.8773

S'S = 2 pi – (azimut de Q1 + CS') = 360 – (319.2185 + 26.363) = 14.4185

sin LE = sin ep sin Lg / cos f = sin 23.4379 sin 87.297 / cos 43 et LE = 32.905

S'L = LE + pi / 2 – S'S = 32.905 + 90 – 14.4185 = 108.4865

L = 49.1736° donné par le programme Régiomontanus, epsilon = 23.4379 en avril 2010

tg JL = 1 / ((cos L / sin S'L tg M) + sin L / tg S'L)

JL = 40.5664° à soustraire de la longitude de l'ascendant: 87.297 – 40.5664 = 46.7305 ou

46.7305 – 30 (Bélier) = 16.7305° ou

Taureau 16° 43' et

La grandeur écliptique de M12 = JL = 40.5664°

Les tables donnent pour 22h13 sidérale à 43° : 16°26'

Calcul de JL et M pour la maison XI

On conserve: Longitude écliptique de l'ascendant = 87.297° gémeaux; temps sidéral = 22h 13' = 333.2427° epsilon = 23.4379° L = 49.1736

Ici on prend t = 1/3 asd ce qui pour Q correspond à 37.948° (t = 360 - 37.948 = 322.052) et pour Q1 à 22.046 (t = 337.954)

hQ = 53.1689 AzQ = 289.7462 hQ1 = 20.5289 AzQ1 = 338.424 dA = 48.6778

tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS' = 14.4929

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M = 56.2442

S'S = 2 pi – (azimut de Q1 + CS') = 360 – (338.424 + 14.4929) = 7.0831

S'L = LE + pi / 2 – S'S = 32.905 + 90 – 7.0831 = 115.8219

et tg JL = 1 / ((cos L / sin S'L tg M) + sin L / tg S'L) d'où JL = 83.2002 à déduire de la longitude de l'ascendant: 8

7.297 – 83.2002 = 4.0967 Bélier (4°5').

Les tables donnent pour 22h 13' sidérale 4° 12'.

M11 = JL11 - JL 12 = 83.2002 - 40.566 = 42.6342 cuspide 4.0967 Bélier (4°5').

Pointe de la maison X

Celle-ci correspond au méridien. Q et Q1 y sont. CS' est alors égal à 0 et tg M = tg hQ1 / sin CS' = tg hQ1 / 0 = infini. M est donc égal à pi / 2.

On a vu que tg JL dans ce cas est égale à tg S'L / sin L S' est en SS et SS' = 0 et

S'L égale ici LE + pi / 2 = 32.905 + 90 = 122.905 (azimut de l'ascendant = 360 – 122.905 = 237.095°) d'où

tg JL = tg 122.905 / sin 49.1736 et JL = 116.0873

à déduire de la longitude de l'ascendant: 87.297 – 116.0873 = -28.7903 ou 360 - 28.7903 = 331.2097 ° ou 331°12' ou 1° 12' Poissons. (Milieu du Ciel)

Comme attendu ce résultat est identique à celui obtenu par la domification de Régiomontanus et de Campanus. Les tables donnent 1° 13' Poissons.

M10 = JL10 - JL11 = 116.0873 – 83.2002 = 32.8871 Cuspide 1° 12' Poissons. (Milieu du Ciel)

Pointes IX, VIII et VII

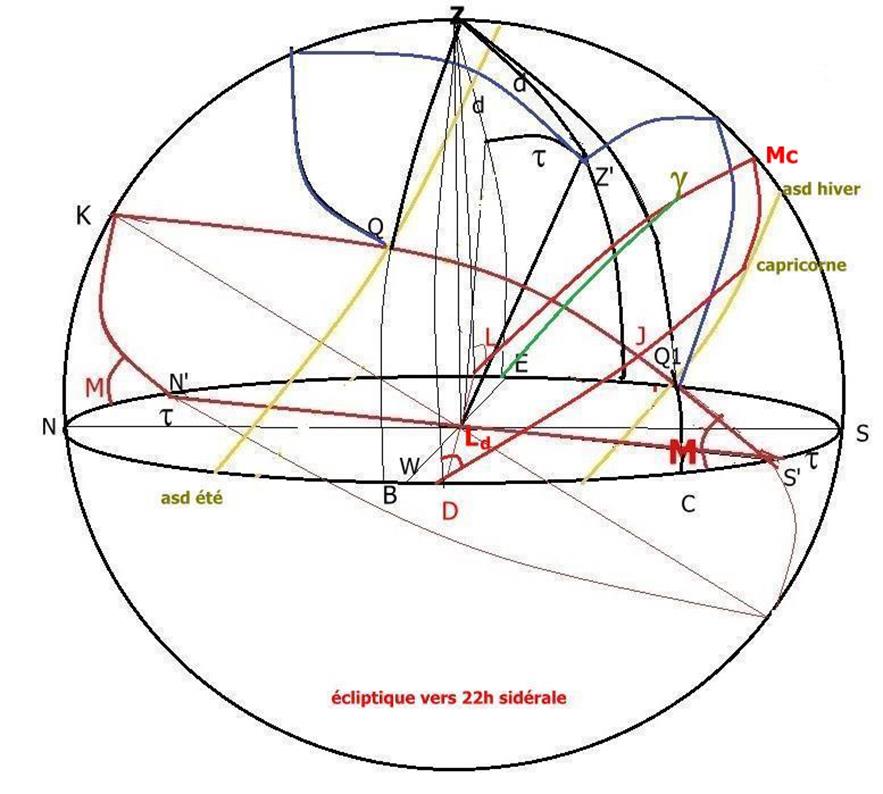fig 16

Pointe VIII

Nous reprenons le cas de figure d'une naissance survenue à 22h 13 sidérale. Le capricorne est sur l'arc semi-diurne de l'après-midi et le descendant est en D.

sa longitude est celle de l'ascendant augmentée de 180°. Elle est donc égale à 87.297 + 180 = 267.297°.

LE = WD car WE et LD sont des diamètres de grands cercles passant donc par le centre de la sphère et donnant des angles opposés

égaux sur le grand cercle commun de l'horizon. Mais WD est ici dans le quart sud ouest de l'horizon (l'ascendant étant décalé de pi dans le quart nord est).

La valeur de S'D est donc de WS - WD - S'S. WS = pi / 2 (cardinal Ouest par où passe l'équateur céleste)

S'S = azimut de Q1 - CS' = t

et S'D = pi / 2 – (WD +S'S)

Ici le cercle N'KQQ1S' est obtenu en faisant incliner le cercle horizon d'un angle d vers l'Est puis en faisant pivoter

le point sud de l'axe méridien NS d'un angle t vers le nord-ouest de façon à faire passer ce cercle par les points Q et Q1

par les 2/3 des asd été et hiver d'après-midi. Le pôle Z' de ce cercle est donc orienté vers le sud-est.

La démonstration permettant de quantifier les valeurs de CS' et de M est absolument identique à celle des maisons XII à X.

tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS' ; S'S = AzQ1 – CS' = t

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M

Les angle L et Ld sont égaux. Ce sont les angles faits entre le vertical et l'écliptique à leur point commun avec l'horizon.

Les triangles ZLMc et ZDMc montrent cela

En effet on a sin L / sin ZMc = sin ZL / sin LMc d'où sin L = sin ZMc / sin LMc et sin Ld / sin ZMc = sin ZD / sin DMc

= sin ZD / sin (pi – LMc) et sin Ld = sin ZMc / sin LMc

d'où sin L = sin Ld et L = Ld L ne peut être plus grand que pi / 2 donc il n'y a aucune ambiguité quand à l'arc sinus de Ld.

Considérons le triangle sphérique DJS'. En remplaçant le point L (lever de l'ascendant) par D (coucher du descendant)

on obtient exactement les mêmes calculs que ci-dessus et on retrouve la même relation:

tg JD = 1 / (cos Ld / (sin S'D tg M) + sin Ld / tg S'D)

S'D (S'D = pi / 2 – (WD +S'S) ) étant différent de S'L (S'L = LE + pi / 2 – S'S )

on trouvera JD différent de JL.

Valeurs constantes: M = 25.8773 , epsilon = 23.4379 CS' = 26.363

S'D = 90 - 32.905 - 40.7814 = 16.3136

Dans McDS on a DS = DS' + S'S = WS – WD = pi / 2 - 32.905 = 57.095

La hauteur du milieu du ciel SMc est égale à pi / 2 – ZMc et cos ZMc = cos L sin LMc (voir plus bas les compléments utiles)

LMc est l'arc JL compris entre l'horizon et la pointe X. Sa valeur a été trouvée égale à 116.0873.

cos ZMc = cos 49.17 sin 116.0873 et ZMc = 54.04 et SMc = 90 – 54.04 = 35.959

L'arc DMc est égal à pi – JL (X) = 180 – 116.0873 = 63.9127°. Ld = L = 49.1736

Ici on prend t = 2/3 asd ce qui pour Q correspond à 75.8968° et pour Q1 à 44.1031

hQ = 25.7708 AzQ = 98.8424 hQ1 = 12.1561 AzQ1 = 40.7814 dA = 58.0609

tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS' = 26.363

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M = 25.8773

S'S = azimut de Q1 - CS' = 40.7814 - 26.363) = 14.41837

sin LE = sin ep sin Lg / cos f = sin 23.4379 sin 87.297 / cos 43 et LE = 32.905

S'D = pi / 2 – (WD + S'S) = 90 -32.905 - 14.41837 = 42.6766 Ld = L = 49.1736

tg JD = 1 / ((cos Ld / sin S'D tg M) + sin Ld / tg S'D)

On trouve alors JD = 19.5961° à ajouter à la longitude du descendant: 267.297 + 19.5961 = 286.8931° ou 16.8931° (16°53' Capricorne)

M7 = JD = 19.5961 et Cuspide 8 = 286.8931° ou 16.8931° (16°53' Capricorne)

Pointe IX

Cette pointe correspond aux tiers des arcs semi-diurnes été et hiver. t = 37.9484 pour l'été et 22.0515 pour l'hiver)

hQ = 53.1753 AzQ = 70.2541 hQ1 = 20.5274 AzQ1 = 21.5779 dA = 48.6762 Ld = L = 49.1736

tg CS' = sin dA / (tg hQ / tg hQ1 – cos dA) d'où CS' = 14.4873

Par suite tg M = tg Q1C / sin CS' = tg hQ1 / sin CS' d'où M = 56.2522

S'S = azimut de Q1 - CS' = t = 21.5779 – 14.4873 = 7.0906

et S'D = pi / 2 – (WD +S'S) = 90 – 32.905 – 7.0906 = 50.0044

et tg DJ = 1 / ((cos Ld / sin S'D tg M) + sin Ld / tg S'D)

d'où DJ = 39.6883 à ajouter à la longitude du descendant: 267.297 + 39.6883 = 306.9853° ou 6°59' Verseau)

M8 vaut donc 39.6883° - 19.5961= 20.1° et pointe 9 = 6°59' Verseau

et M9 vaut la différence entre la pointe IX et le milieu du ciel: 331.2097 - 306.9852 = 24.2244)

Pointe VII C'est le grand cercle de l'horizon correspondant au descendant : La pointe est donc égale à 87.297 + 180 = 267.297 (27° 58' Sagittaire)

Pointe VI

Nous nous trouvons dans le cas de la maison XII avec les mêmes angles. La partie "longue" du zodiaque LMc se retrouve

ici en DFc où Fc est le fond du ciel. On en déduira que la portion DJ de la maison VI est égale à la portion LJ de la

maison XII et il en est de même pour les autres maisons:

On pourra écrire que M12 = M6, M11 = M5, M10 = M4, M9 = M3, M8 = M2, et M7 = M1

avec cuspide 12 : JL = 40.5664° à soustraire de la longitude de l'ascendant: 87.297 – 40.5664 = 46.7305 ou 46.7305 – 30 (Bélier)

= 16.7305° Taureau 16° 43' et

M12 = JL = 40.5664 cuspide 12 = 46.7305 ou 16° 43' taureau

cuspide 11 : JL = 83.2002 87.297 – 83.2002 = 4.0967 Bélier (4°5'). Les tables donnent pour 22h 13' sidérale 4° 12'. Donc résultat conforme.

43Cuspide 10 JL = 116.0873

M10 : 87.297 – 116.0873 = -28.7903 ou 360 - 28.7903 = 331.2097 ° ou 331°12' ou 1° 12' Poissons. Les tables donnent 1° 13' Poissons.

M10 = JL10 - JL11 = 116.0873 – 83.2002 = 32.8871 cuspide 10 = 331°12' ou 1° 12' Poissons

M7 : on trouve JD = 19.5883° à ajouter à la longitude du descendant: 267.297 + 19.5883 = 286.8853° ou 16.8853° (16°53' Capricorne)

M7 vaut donc 19.5961° cuspide 7 = 267.297 longitude du descendant ou 27° 17' SAGITAIRE

et cuspide 8 = 267.297 + 19.5961= 286.8931° ou 16.8931° (16°53' Capricorne)

M8: DJ = 39.6883 à ajouter à la longitude du descendant: 267.297 + 39.6883 = 306.9853° ou cuspide 9 (6°59' Capricorne)

M8 vaut donc 39.6883° - 19.5961 = 20.0922° cuspide 9 = 286.8931 + 20.0922= 306.9853° ou 6.9853° (6°59' Capricorne)

M9 : vaut la différence entre la pointe IX et le milieu du ciel: 331.2097 - 306.9853 = 24.2244

Cuspide 9 = 306.9853 ou 6.953 Capricorne (6° 57')

M6 = M12 ; JL = 40.5664 et cuspide M6 = longitude du descendant – 40.5664 ou

267.297 – 40.5664 = 226.7306° ou 16° 43' scorpion

M5 = M11; JL = 42.6338 et cuspide M5 = 226.7306 – 42.6338 = 184.0968 ou 4° 5' balance

M4 = M10; JL =32.8871 CUSPIDE M4 = 184.0968 - 32.8871 = 151.2097 ou 1° 12' VIERGE

M3 = M9; JL = 24.2245 CUSPIDE M3 = 151.2097 - 24.2245 = 126.9852 ou 6° 59' LION

M2 = M8; JL = 20.1 CUSPIDE M2 = 126.9852 - 20.0922 = 106.893 ou 16° 53' CANCER

M1 = M7; JL = 19.5961 CUSPIDE M1 = 106.893 - 19.5961 = 87.297 ou 27°17' GEMEAUX (ASCENDANT)

Ces résultats sont conformes aux tables du commerce.

Rappelons que les relations établies pour le calcul de Zg , B permettant le calcul de l'arc d'écliptique Lg (longitude de l'ascendant)

restent applicables telles quelles, quel que soit le temps sidéral en rapport avec l'ascendant.

Par contre l'étude nous a montré qu'entre 18h et 0h (en passant par 18h) dans la relation donnant sin l il fallait prendre la valeur

B + e et entre 0 et 12h en passant par 6h il fallait prendre la valeur B – e (e inclinaison de l'écliptque sur l'équateur).

La relation sin Lg = cos Zg / cos L n'entraine aucune correction entre 18h et 6h en passant par 0h car à un moment donné l'arc Lg va dépasser 90° et

sin Lg = sin (pi – Lg). La calculette fournit le plus petit angle. On a démontré plus haut que si B + e < pi / 2 --> Lg < pi / 2:

on prend l'angle donné par la calculette et

si B + e > pi / 2 --> Lg > pi / 2 on prend pi – l'angle obtenu avec la calculette. (période du sinus).

Entre 0h et 6h sidérale Lg est constamment > pi / 2 et égal à pi à 6h. On prendra également pi – Lg obtenu avec la calculette.

De 6 h à 12 h sidérale Lg est compris entre pi et 3pi/2. L’ordinateur donnera l’arc -Lg correspondant : on posera alors dans le programme

Lg = pi - Lg (puisque Lg a une valeur négative. Exemple: sin 240 <=> arc sinus 240 = - 60 et 240 = 180 -(-60) )

Enfin entre 12h et 18h sidérale, à un certain moment, Lg va dépasser la valeur 3pi/2.

si Lg < 3pi/2 on a vu qu’il fallait prendre Lg = pi - Lg (ici Lg est <0).

si Lg > 3pi/2 l’ordinateur donne la valeur angulaire minimale

(par exemple sin 300° et arc sin 300° = -60°)

donc il nous faudra écrire dans le programme : Lg = 2pi+Lg (puisque Lg est <0)

Lorsque Lg = 3pi/2 on a sin Lg = cos Z / cos L = -1 d’où Z = pi-L et (3’) permet d’écrire:

sin L = sin (pi-L) sin (B+ep) ==> sin (B+ep) = 1 et B+ep = pi/2

On a vu que dans ce cas B décroît de pi/2 à f. On en déduit que si B+e > pi/2 alors Lg < 3pi/2 et on emploiera alors Lg = pi-Lg.

si B+e < pi/2 alors Lg > 3pi/2 et on emploiera Lg = 2pi+Lg.

Lorsque gamma est au-dessus de l'horizon (18h à 6h en passant par 0h) l'étude sur la domification de Régiomontanus nous a montré que

sin LE = sin e sin Lg / cos f et que lorsque gamma est sous l'horizon (6h à 18h en passant par 12h) sin LE = - sin ep sin Lg / cos f.

Il faudra donc tenir compte de ces valeurs en fonction du temps sidéral donné. Entre 18h et 6h sidérale gamma est sur l'horizon.

L'écliptique se lève vers le nord et se couche vers le sud.

On compte LE en valeur absolue et pour les maisons XII, XI et X (maisons du matin) on prend

S'L = pi / 2 + LE – SS'. Pour les maisons XI, VIII et VII (maisons du soir) on prend S'D = pi / 2 – (LE + SS')

Lorsque gamma est sous l'horizon l'écliptique se lève vers le sud et se couche vers le nord.

On prend alors pour les maisons XII, XI et X S'L = pi / 2 – (LE + SS') et pour les maisons IX, VIII et VII

S'D = pi / 2 + LE – SS'

Domification de l'hémisphère sud.

La cuspide 7 dans l'hémisphère nord est le lieu géométrique du descendant comme la cuspide 1 est le lieu de l'ascendant.

Tout astre passant de la maison 7 dans la maison 6 se lèvera au même instant dans l'hémisphère sud

traversant ainsi la cuspide 7 devenue cuspide 1 passant alors de la maison 7 nord devenue maison 1 sud dans la maison 6 nord

devenue maison XII sud et ainsi de suite. Le temps sidéral sera décalé de 12h car compté à partir du méridien sud.

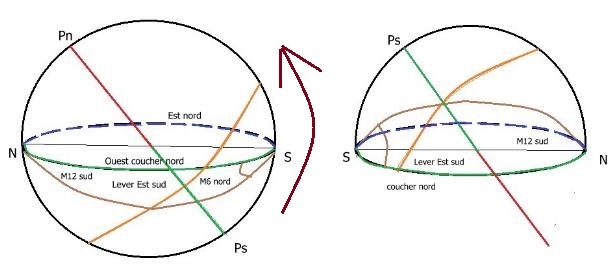
En pratique une fois connu le temps sidéral pour une latitude nord il faudra augmenter celui-ci de 12h puis faire la domification avec le programme habituel.

Ensuite tout en gardant les mêmes résultats numériques il faudra changer l numérotation des maisons comme indiqué ci-dessus:

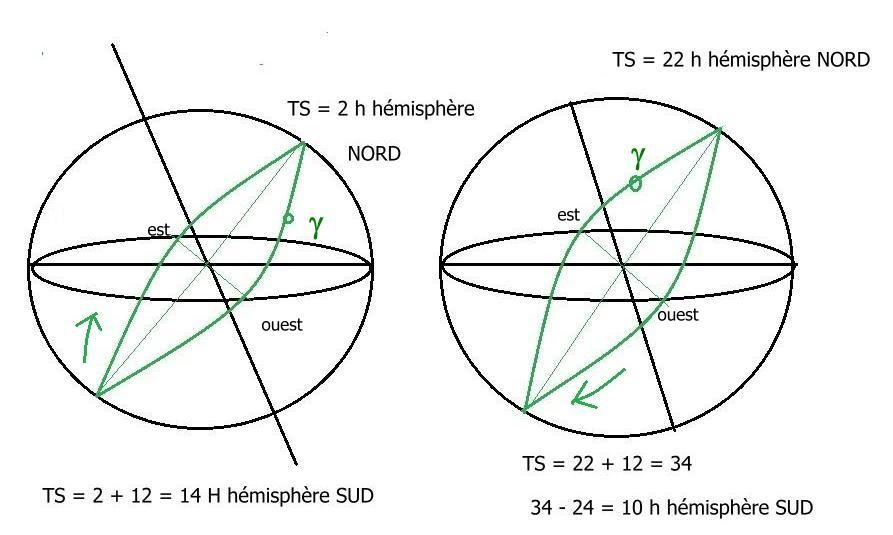
M6 NORD DEVIENT M12 SUD (ou cuspide 6 nord devient cuspide 12 sud)

M5------------------------M11 cuspide 5 devient cuspide 11

M4------------------------M10 cuspide 4 devient cuspide 10

M3-------------------------M9 cuspide 3 devient cuspide 9

M2-------------------------M8 cuspide 2 devient cuspide 8

M1-------------------------M7 cuspide 1 devient cuspide 7

M12------------------------M6 cuspide 12 devient cuspide 6

M11------------------------M5 cuspide 11 devient cuspide 5

M10------------------------M4 cuspide 10 devient cuspide 4

M9--------------------------M3 cuspide 9 devient cuspide 3

M8--------------------------M2 cuspide 8 devient cuspide 2

M7--------------------------M1 cuspide 7 devient cuspide 1

Les Maisons de Placidus et Régiomontanus sur les cadrans solaires

Compléments utiles sur la domification

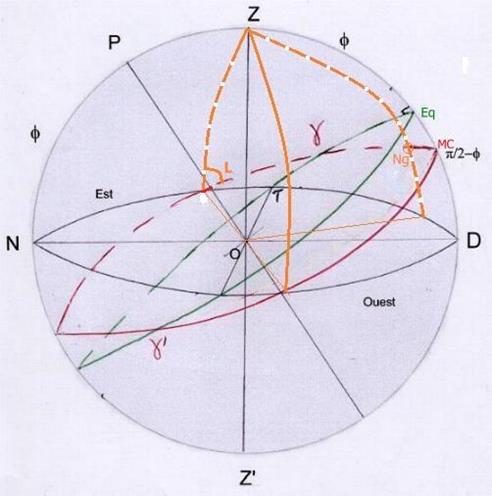
Ecliptique en rouge et équateur en vert

Zodiaque vers 21 h sidérale (gamma se lève à 18 heure sidérale passe au méridien à 24 hs est au cardinal ouest pour

le coucher à 6h sidérale, passe au Fond du Ciel NZ' à 12 hs…)

Le nonagésime Ng partage le zodiaque en deux parties égales sur l'horizon

Le Milieu du Ciel Mc correspond au zodiaque traversé par la méridienne

(cuspide de la maison X en placidus, Régiomontanus…)

L point de l'ascendant sur l'horizon: ce point décrira comme tous les astres un cercle de déclinaison

parallèle à l'équateur céleste.

- Nonagésime

Connaissant la longitude écliptique de l'ascendant (fournie par mon programme de domification) on va retrancher pi/2 pour

avoir le point médian du zodiaque sur l'horizon. Retrancher et non ajouter car le mouvement diurne se fait en sens rétrograde.

Par exemple si la longitude de l'ascendant est de 50° celle du nonagésime correspondant sera de

50-90 = -40° <=> -40+360 = 320°

- Hauteur du nonagésime

Le triangle ZLNg permet d'écrire cos L = cos ZL cos LNg + sin ZL sin LNg cos ZNg

ZL = LNg = pi/2 donc cos L = cos ZNg et ZNg = L connu par ailleurs. (sin L = sin Z sin (B+ep) entre 12h et 24h sidérale et sin L = sin Z sin (B-ep) entre 0h et 12h sidérale (développement dans le travail ci-dessus).

La hauteur du nonagésime est donc égale à PI/2 – L

- Azimut du nonagésime

Il est égal à PI/2 + ou – LT connu par ailleurs; + lorsque gamma est sur l'horizon et – dans le cas contraire

- Déclinaison de l'ascendant.

On démontre par ailleurs que sin d = sin ep sin lo

où d est la déclinaison d'un point de l'écliptique , ep l'angle dièdre fait entre le plan de l'équateur et celui de l'écliptique,

lo étant la longitude écliptique du point considéré.

- Ascension droite a de l'ascendant

cos a = cos lo / cos d

- Angle horaire de l'ascendant

Connaissant le temps sidéral Ts de la naissance l'angle horaire H de l'ascendant est égal à Ts – a

- Arc semi-diurne asd de l'ascendant sur l'horizon de latitude f

Donné par la relation classique asd = arc cos (- tg d tg f)

- Longitude écliptique du Milieu du Ciel

c'est l'arc d'écliptique LS compris entre l'ascendant et la cuspide de la maison X (sur la méridienne).

Cette valeur est donnée dans le travail précédent avec les valeurs des autres paramètres:

tg LS = 1 / (cos L / tg M sin NL - sin L / tg NL) ===> LLS(10)

si M tend vers pi/2 ou 3pi/2 tg M tend vers + ou - l’infini, tg LS tend vers sin NL/-cos NL sinL

= -tg NL / sin L (cuspide maisons 10 et 4).

Connaissant l'ascendant on va retrancher LS pour avoir le Milieu du Ciel.

Retrancher et non ajouter car le mouvement diurne se fait en sens rétrograde.

Par exemple si la longitude de l'ascendant est de 50° et LS = 100° la longitude du Milieu du Ciel sera

de 50 - 100 = -50° + 360 = 310°

-hauteur du Milieu du Ciel

On considère le triangle ZLMc cosZMc = cos ZL cos LMc + sin ZL sin LMc cos L ZL = PI/ 2 et LMc = LS

d'où cos ZMc = sin LS cos L et la hauteur du Milieu du Ciel est PI/2 – ZMc

On aura LS directement en appliquant le programme de domification

Nous nous servirons de ces relations dans le programme informatique REGPLA20.

Nous avons tiré de cette étude géométrique le programme basic ci-dessous.

Les résultats obtenus sont conformes aux tables trouvées dans les éditions commerciales.

3 REM regpla20      25 1 2019 = regpla17 avec correction jlp (n) < à 0 then jlp (n)

= jlp (n) + pi

4 REM   dans les lignes 3960-3980 et 4130-4150 

10 REM REGPLA17 3 3 16 17h 24

20 REM REGPLA16 = REGPLA13 2 3 2016 9h38

30 REM REGPLA12 =REGPLA11 renum 29 2 2016 14h23 ave correction gamma sur et sou

s horizon pour les valeurs sl1,sl2,sl3,sl4 15H 25

40 CLEAR ALL

0 PRINT"Pour domifier l'hémisphère nord, temps sidéral connu ou non, entrer la

latitude avec le signe + ou sans signe."

60 PRINT "Pour domifier l'hémisphère sud entrer la latitude avec le signe - que le temps sidéral soit connu ou non.

Ce signe - quand le TS est connu n'a pas d'i

nfluence sur la domification mais permet l'affichage des bonnes valeurs pour le calcul des azimuts des levers et couchers de l'écliptique"

70 INPUT"Domification Régiomontanus appuyer sur R; Placidus sur P",D$

80 REM la partie horoscope a été supprimée.

90 REM Permet de calculer les valeurs astros (hauteur du nonagésime, azimut, mil

ieu du ciel...) à partir du temps sidéral.

100 REM la partie horoscope a été supprimée.

110 REM Permet de calculer les valeurs astros (hauteur du nonagésime, azimut, milieu du ciel...) à partir du temps sidéral.

120 OPEN"REGPLA17.doc" FOR OUTPUT AS #1

130 GOTO 280

140 IF K<30 THEN QQB$="Bélier":GOTO 260

150 IF K<60 THEN QQB$="Taureau":GOTO 260

160 IF K<90 THEN QQB$="Gémeaux":GOTO 260

170 IF K<120 THEN QQB$="Cancer":GOTO 260

180 IF K<150 THEN QQB$="Lion":GOTO 260

190 IF K<180 THEN QQB$="Vierge":GOTO 260

200 IF K<210 THEN QQB$="Balance":GOTO 260

210 IF K<240 THEN QQB$="Scorpion":GOTO 260

220 IF K<270 THEN QQB$="Sagittaire":GOTO 260

230 IF K<300 THEN QQB$="Capricorne":GOTO 260

240 IF K<330 THEN QQB$="Verseau":GOTO 260

250 IF K>=330 THEN QQB$="Poissons"

260 K=0

270 RETURN

280 INPUT"Prenom, Nom, né(e) à xyz ?",H$:PRINT #1,H$

290 PRINT #1,

300 CLS:DEFDBL A-Z:PI=4#*ATN(1#)

310 TSO=.2782986111#:REM temps sidéral à Greenwich le 1/1/1900 à 0h (6h40'45'' t

ransformé en jour)

320 PRINT"Latitude et longitude en ° centésimaux: + pour le Nord et pour l'Ouest"

330 PRINT"- pour le Sud et l'Est"

340 INPUT"Latitude, Longitude ?",FF,LGT

350 F=FF*PI/180#:IF F>0 THEN PRINT #1,FF;"° Latitude Nord" ELSE PRINT #1,FF;"° Latitude Sud":F=ABS(F)

360 IF LGT>0 THEN PRINT #1,LGT;"° Longitude Ouest" ELSE PRINT #1,LGT;"° Longitude Est"

370 OPTION BASE 1

380 DIM TE(12):DIM M(12):DIM NE(12):DIM LLS(12):DIM LS(12):DIM NNE(12):DIM MA(12)

390 INPUT"Temps sidéral connu: appuyez sur y: inconnu sur n",Q$

400 IF Q$="n" THEN 420

410 INPUT "Année de 1900 à 2050, mois de 1 à 12, jour",A,MO,J:GOTO 990

420 INPUT"Année de 1900 à 2050, mois de 1 à 12, jour, heures, minutes, secondes",A,MO,J,H,MN,SC

430 PRINT #1,"Temps civil: ";J;"/";MO;"/";A;" ";H;"H";MN;"'";SC;"''"

440 PRINT "Entrer le numéro du fuseau horaire avec son signe:- pour l'est (-1 zone France;-10 pour la zone de Melbourne

par exemple ou + n°du FUSEAU à l'ouest de Greenwich"

450 PRINT "Entrer si nécessaire la correction arbitraire locale; par exemple +1h en ETE

(le n° du fuseau tient compte du supplément de 1h en hiver)"

460 INPUT"n° du fuseau avec son signe?",NF

470 INPUT"Correction arbitraire éventuelle: par exemple + 1 en ETE en France ?",C:C=-C

480 PRINT #1,"correction horaire = ";C

490 GOTO 560

500 REM on trouve le temps universel par rapport à l'heure légale d'un endroit quelconque de la planète.

510 REM c'est en effet à partir de ce TU que se calcule le temps sidéral.

520 REM par exemple en France on prend - 1 heure l'hiver (fuseau 1) et - 2 heures l'été (fuseau 2).

530 REM Pour Melbourne il faudrait prendre -10 car fuseau 10 à l'EST (il n'y a pas d'heure d'été).

540 REM le temps universel tu est la différence entre le temps civil de la montre et le temps du fuseau.

Par exemple lorsqu'il est 9h20 à Paris il esr 8h20 à Greenwich

550 REM lorsqu'il est 11h50 à Melbourne il est 1h50 à Greenwich

560 TU=H+MN/60#+SC/3600#+NF+C:TU=TU/24#:REM transformation de tu en jour

570 PRINT #1,"TEMPS UNIVERSEL = ";TU*24#;" h = ";TU;" jour":PRINT "TEMPS UNIVERSEL = ";TU*24#;" h = ";TU;" jour"

580 IF A>2050 THEN PRINT"l'année doit être <= 2050":GOTO 420

590 IF A<1900 THEN PRINT"l'année doit être >= 1900":GOTO 420

600 AN=2049:IF A=1900 THEN BIS=0:GOTO 650

610 FOR J%=38 TO 1 STEP -1

620 IF A>=AN THEN BIS=J%-1:J%=1:GOTO 640

630 AN=AN-4

640 NEXT J%

650 IF MO=1 THEN MOI=0:GOTO 770

660 IF MO=2 THEN MOI=31:GOTO 770

670 IF MO=3 THEN MOI=59:GOTO 770

680 IF MO=4 THEN MOI=90:GOTO 770

690 IF MO=5 THEN MOI=120:GOTO 770

700 IF MO=6 THEN MOI=151:GOTO 770

710 IF MO=7 THEN MOI=181:GOTO 770

720 IF MO=8 THEN MOI=212:GOTO 770

730 IF MO=9 THEN MOI=243:GOTO 770

740 IF MO=10 THEN MOI=273:GOTO 770

750 IF MO=11 THEN MOI=304:GOTO 770

760 IF MO=12 THEN MOI=334

770 NJ=(A-1900)*365#+BIS+MOI+J-1#+TU

780 NJS=NJ*1.002737905#-LGT/(15#*24#):REM les longitudes sont du temps sidéraldonc inutile de les * par 1.002737905

790 REM (facteur de transformation de temps solaire en temps sidéral j sol = jsid + 256.555 sec)

800 REM 1 jour sidéral <=> 86400/86636.55 = .9972696 jour solaire moyen.

LGT/15/24 <=> (LGT*4)/60/24 (1°=4'divisé par 60=> heures et divisé par 24=>jour)

810 AAA = 1904

820 FOR K%=1 TO 37

830 IF A=AAA THEN IF MO>2 THEN NJ=NJ+1

840 AAA=AAA+4

850 NEXT K%:REM cela permet de rajouter 1 jour à la dernière année bissextile quand le mois de naissance dépasse février.

860 REM Par exemple les lignes 520-560 donneront bis=36 pour 2048 (37 aprés février)

870 TS=NJS-FIX(NJS)+TSO

880 TS=TS*24#:IF TS>24# THEN TS=TS-24#

890 IF FF>0 THEN 950

900 TS=TS+12#:REM latitude sud

910 IF TS>24 THEN TS=TS-24

920 TTS=TS:TTTS=TTS-12: IF TTTS<0 THEN TTTS=TTTS+12

930 PRINT "latitude sud : dans l'hémisphère sud le temps sidéral est ";TTS;"égal à ";TTTS;" nord +12.

On domifie alors l'hémisphère nord avec ce TS sud et on réappareille les numéros des cuspides (voir l'étude)"

940 PRINT #1,"latitude sud : dans l'hémisphère sud le temps sidéral est ";TTS;"égal à ";TTTS;" nord + 12.

On domifie alors l'hémisphère nord avec ce TS et on réappareille les numéros des cuspides (voir l'étude)"

950 PRINT"Temps sidéral= ";TS;"<=>";FIX(TS);"H";(TS-FIX(TS))*60#;"min."

960 PRINT #1,"Temps sidéral= ";TS;"<=>";FIX(TS);"H";(TS-FIX(TS))*60#;"min."

970 T=TS*15#:IF T=360# THEN T=0#

980 TT=T*PI/180#

990 REM L'inclinaison Ep de l'équateur céleste sur l'écliptique (orbite du soleil autour de la terre (ou de la terre autour du soleil))

1000 REM varie au cours des ans très insensiblement. Elle diminuera pendant encore 15000 ans puis croîtra à nouveau

1010 REM pendant 50000 ans. Etc...Cette variation est traduite avec une bonne approximation par la formule

1020 REM Epsilon=23°27'8'',26 -0'',46845*t t étant compté en années depuis le 1/1/1900.

1030 ANT=A-1900+(MO-1#)/12#+(J-1#)/365#

1040 EP=23.45233889#-(.46845#*ANT)/3600#:PRINT #1,"epsilon = ";EP;"°":EP=EP*PI/180#:REM 23.45233889

= 23°27'8,42'' valeur d'epsilon le 1/1/1900.

1050 GOTO 1770

1060 NNE(I%)=-SIN(TE(I%))*SIN(F):IF NNE(I%)=0 THEN NE(I%)=PI/2#:GOTO 1080

1070 NE(I%)=ATN(SQR(1#-NNE(I%)^2#)/NNE(I%)):IF NNE(I%)<0 THEN NE(I%)=NE(I%)+PI:R

EM NE est toujours<pi

1080 MA(I%)=COS(TE(I%))/SIN(NE(I%)):IF I%=10 THEN M(I%)=PI/2#:RETURN

1090 IF I%=7 THEN M(I%)=PI:RETURN

1100 IF I%=4 THEN M(I%)=3#*PI/2#:RETURN

1110 IF I%=1 THEN M(I%)=2#*PI:RETURN

1120 M(I%)=ATN(SQR(1#-MA(I%)^2#)/MA(I%))

1130 IF 3#*PI/2#<TE(I%) THEN IF TE(I%)<2#*PI THEN M(I%)=2#*PI-M(I%):RETURN

1140 REM pèriode du cosinus : maisons 3,2,1

1150 IF PI<TE(I%) THEN IF TE(I%)<3#*PI/2# THEN M(I%)=PI-M(I%):RETURN

1160 REM maisons 6,5,4

1170 IF PI/2#<TE(I%) THEN IF TE(I%)<PI THEN M(I%)=M(I%)+PI:RETURN:REM maisons 9,8,7

1180 RETURN:REM maisons 12,11,10 ; te(i%)<pi/2

1190 LT=SIN(LLG)*SIN(EP)/COS(F):LT=ATN(LT/SQR(1#-LT^2#)):LN=PI/2#-LT

1200 REM maisons 12 à 1 Gamma sur l'horizon (tt>3pi/2 ou <pi/2).

1210 RETURN

1220 LT=-SIN(LLG)*SIN(EP)/COS(F):LT=ATN(LT/SQR(1#-LT^2#)):LN=PI/2#+LT

:REM maisons 12 à 1 Gamma sous l'horizon (pi/2<tt<3pi/2).

1230 REM donc LT constamment > 0 car -sin LG >0 (pi<LG<2 pi) et epsilon est compté en valeur absolue

1240 RETURN

1250 IF T=90# THEN PRINT #1,"HAUTEUR DU MILIEU DU CIEL = ";FIX((PI/2#-F+EP)*1800

1260 IF T=270# THEN PRINT #1,"HAUTEUR DU MILIEU DU CIEL = ";FIX((PI/2#-F-EP)*180

00#/PI)/100#;" °"

1270 ZMC=SIN(LLS(10))*COS(LL):ZMC=ATN(SQR(1#-ZMC^2#)/ZMC):ZMC=PI/2#-ZMC

1280 PRINT #1,"Hauteur du Milieu du Ciel = ";FIX(ZMC*18000#/PI)/100#;"°"

1290 RETURN

1300 LS(I%)=TAN(M(I%))*SIN(LN)/(COS(LL)-COS(LN)*TAN(M(I%))*SIN(LL))

1310 IF I%=7# THEN LS(I%)=0:GOTO 1330

1320 IF I%=1# THEN LS(I%)=0

1330 LLS(I%)=ATN(LS(I%))

1340 IF I%<10 THEN 1370:REM maisons 10,11,12

1350 IF LS(I%)<0 THEN LLS(I%)=LLS(I%)+PI

1360 GOTO 1460

1370 IF I%<7 THEN 1400:REM maisons 7,8,9

1380 IF LS(I%)<=0 THEN LLS(I%)=LLS(I%)+PI:REM <=0 car si M=pi(maison 7) tan (pi)=0 et tan(ls)=0 d'où atn(0)=0.

Donc il faut dans ce cas rajoutter pi.

1390 GOTO 1460

1400 IF I% <4 THEN 1440:REM maisons 4,5,6

1410 IF LS(I%)>0 THEN LLS(I%)=LLS(I%)+PI:GOTO 1460

1420 LLS(I%)=2#*PI+LLS(I%):GOTO 1460

1430 REM maisons 1,2,3

1440 IF LS(I%)>0 THEN LLS(I%)=LLS(I%)+PI:GOTO 1460

1450 LLS(I%)=2#*PI+LLS(I%)

1460 RETURN

1470 REM calcul de Z (h=pi/2-z)

1480 Z=COS(F)*COS(TT):ZZ=ATN(SQR(1#-Z^2#)/Z)

1490 IF Z<0# THEN ZZ=ZZ+PI

1500 RETURN

1510 REM calcul de B

1520 B=SIN(F)/SIN(ZZ):BB=ATN(B/SQR(1#-B^2#))

1530 IF BB<0# THEN BB=BB+PI

1540 RETURN

1550 REM calcul de l 0 à 12H hémisphère NORD

1560 L=SIN(ZZ)*SIN(BB-EP):LL=ATN(L/SQR(1#-L^2#))

1570 RETURN

1580 REM calcul de l 12 à 24H hémisphère nord

1590 L=SIN(ZZ)*SIN(BB+EP):LL=ATN(L/SQR(1#-L^2#))

1600 RETURN

1610 REM longitudes des levers et couchers de l'écliptique ainsi que le nonagésime

1620 LG=COS(ZZ)/COS(LL):LLG=ATN(LG/SQR(1#-LG^2#))

1630 RETURN

1640 CLG=LLG+PI:IF CLG>2#*PI THEN CLG=CLG-2#*PI

1650 NONA=CLG+PI/2#:IF NONA>2#*PI THEN NONA=NONA-2#*PI

1660 LLLG=FIX(LLG*18000#/PI)/100#:CLG=FIX(CLG*18000#/PI)/100#:NONA=FIX(NONA*18000#/PI)/100#

1670 RETURN

1680 REM cas où TS =0 ou 180° (0h ou 12h).

1690 L=SIN(F)*COS(EP):LL=ATN(L/SQR(1#-L^2#)):LG=COS(F)/COS(LL)

1700 LLG=ATN(LG/SQR(1#-LG^2#))

1710 IF T=180# THEN LLG=-LLG:REM on a vu que dans ce cas sin lg = -cos(f)/cos(l)

1720 LLG=PI-LLG:REM t=0 ou t=180 <=> llg toujours > pi/2 et < 3*pi/2

1730 CLG=LLG+PI:IF CLG>2#*PI THEN CLG=CLG-2#*PI

1740 NONA=CLG+PI/2#:IF NONA>2#*PI THEN NONA=NONA-2#*PI

1750 LLLG=FIX(LLG*18000#/PI)/100#:CLG=FIX(CLG*18000#/PI)/100#:NONA=FIX(NONA*18000#/PI)/100#

1760 GOTO 1990

1770 IF Q$="n" THEN GOTO 1830

1780 INPUT "Temps sidéral en heures et minutes :h,m ?",H,M:

1790 TS=(H*60#+M)/60#:T=TS*15#:IF T=360# THEN T=0#

1800 REM 1 heure=15° et (h*60+m)/60<=>conversion heures sexagésimales en heures décimales.

1810 PRINT #1,"Temps sidéral = ";H;" H ";M;" m"

1820 TT=T*PI/180#

1830 GOSUB 1480

1840 IF T=0# THEN 1690

1850 IF T=180# THEN 1690

1860 GOSUB 1520:REM CALCUL DE BB

1870 IF TS<12# THEN GOSUB 1560:GOTO 1890:REM CALCUL DE LL 0<ts<12 hémis nord

1880 GOSUB 1590:REM ts>12

1890 GOSUB 1620

1900 IF 0#<TS THEN IF TS<12# THEN LLG=PI-LLG:GOSUB 1640:GOTO 1990

1910 IF 12#<TS THEN IF TS<18# THEN 1950

1920 IF BB+EP>=PI/2# THEN LLG=PI-LLG:GOSUB 1640:GOTO 1990

1930 REM 18<ts<24 <=> llg>90°

1940 GOSUB 1640:GOTO 1990:REM 18<TS<24 llg<90° llg=llg

1950 IF BB+EP>=PI/2# THEN LLG=PI-LLG:GOSUB 1640:GOTO 1990

1960 REM 12<ts<18 llg<270°

1970 LLG=2#*PI+LLG:GOSUB 1640
1980 REM 12<ts<18 llg>270° (+llg car llgest<0)

1990 K=NONA:GOSUB 140:NNG$=QQB$

2000 K=LLLG:GOSUB 140:ASLLG$=QQB$

2010 K=CLG:GOSUB 140:DESLLG$=QQB$

2020 NONAHS=NONA+180#: IF NONAHS>360# THEN NONAHS=NONAHS-360#

2030 K=NONAHS:GOSUB 140:NNGHS$=QQB$

2040 LLLGHS=LLLG+180#:IF LLLGHS>360# THEN LLLGHS=LLLGHS-360#

2050 CLGHS=CLG+180#:IF CLGHS>360# THEN CLGHS=CLGHS-360#

2060 IF FF<0 THEN 2140

2070 PRINT "F>0: hémisphère nord: Longitude du lever de l'écliptique = ";LLLG;" ";ASLLG$

2080 PRINT #1,"F>0: hémisphère nord: Longitude du lever de l'écliptique = ";LLLG;" ";ASLLG$

2090 PRINT "Longitude du coucher de l'écliptique = ";CLG;"°";DESLLG$

2100 PRINT#1,"Longitude du coucher de l'écliptique = ";CLG;"°";DESLLG$

2110 PRINT "Nonagésime = ";NONA;" ";NNG$

2120 PRINT #1,"Nonagésime hémisphère Nord = ";NONA;" ";NNG$

2130 GOTO 2210

2140 PRINT "F<0: hémispère sud: Longitude du lever de l'écliptique = ";LLLGHS;" ";DESLLG$

2150 PRINT #1,"F<0: hémisphère sud: Longitude du lever de l'écliptique = ";LLLGHS;" ";DESLLG$

2160 PRINT #1,"Longitude du coucher de l'écliptique = ";CLGHS;" ";ASLLG$

2170 PRINT "Longitude du coucher de l'écliptique = ";CLGHS;" ";ASLLG$

2180 PRINT #1,"Nonagésime hémisphère Sud = ";NONAHS;" ";NNGHS$

2190 PRINT "Nonagésime hémisphère Sud = ";NONAHS;" ";NNGHS$

2200 REM Calcul des maisons hémis nord2

210 IF TT<PI/2# THEN GOSUB 1190:GOTO 2240:REM Gamma sur l'horizon.

2220 IF TT>3#*PI/2# THEN GOSUB 1190:GOTO 2240:REM Gamma sur l'horizon.

2230 GOSUB 1220:REM tt>pi/2 ou<3pi/2 <=>Gamma sous l'horizon.

2240 FOR I%=12 TO 1 STEP -1

2250 IF I%=12 THEN TE(I%)=PI/6#:REM 30*pi/180

2260 IF I%=11 THEN TE(I%)=PI/3#:REM 60*PI/180

2270 IF I%=10 THEN TE(I%)=PI/2#:REM 90*pi/180

2280 IF I%=9 THEN TE(I%)=2#*PI/3#

2290 IF I%=8 THEN TE(I%)=5#*PI/6#

2300 IF I%=7 THEN TE(I%)=PI

2310 IF I%=6 THEN TE(I%)=7#*PI/6#

2320 IF I%=5 THEN TE(I%)=4#*PI/3#

2330 IF I%=4 THEN TE(I%)=3#*PI/2#

2340 IF I%=3 THEN TE(I%)=5#*PI/3#

2350 IF I%=2 THEN TE(I%)=11#*PI/6#

2360 IF I%=1 THEN TE(I%)=2#*PI

2370 GOSUB 1060:REM maisons hémis nord

2380 GOSUB 1300

2390 NEXT I%

2400 REM An=limite supèrieure de la maison n; llg étant la longitude de l'ascendant. Par exemple A12 est la cuspide de la maison XII;

A8 celle de la maison VIII.

2410 CUSPA12=LLG-LLS(12):IF CUSPA12<0 THEN CUSPA12=CUSPA12+2#*PI

2420 K=(CUSPA12*18000/PI)/100:GOSUB 140

2430 QB12N$=QQB$

2440 VALA12=LLS(12)

2450 CUSPA11=LLG-LLS(11):IF CUSPA11<0 THEN CUSPA11=CUSPA11+2#*PI

2460 K=(CUSPA11*18000/PI)/100:GOSUB 140

2470 QB11N$=QQB$

2480 VALA11=LLS(11)-LLS(12)

2490 CUSPA10=LLG-LLS(10):IF CUSPA10<0 THEN CUSPA10=CUSPA10+2#*PI

2500 K=(CUSPA10*18000/PI)/100:GOSUB 140

2510 QB10N$=QQB$

2520 VALA10=LLS(10)-LLS(11)

2530 CUSPA9=LLG-LLS(9):IF CUSPA9<0 THEN CUSPA9=CUSPA9+2#*PI

2540 K=(CUSPA9*18000/PI)/100:GOSUB 140

2550 QB9N$=QQB$

2560 VALA9=LLS(9)-LLS(10)

2570 CUSPA8=LLG-LLS(8):IF CUSPA8<0 THEN CUSPA8=CUSPA8+2#*PI

2580 K=(CUSPA8*18000/PI)/100:GOSUB 140

2590 QB8N$=QQB$

2600 VALA8=LLS(8)-LLS(9)

2610 CUSPA7=LLG-LLS(7):IF CUSPA7<0 THEN CUSPA7=CUSPA7+2#*PI

2620 K=(CUSPA7*18000/PI)/100:GOSUB 140

2630 QB7N$=QQB$

2640 VALA7=LLS(7)-LLS(8)

2650 CUSPA6=LLG-LLS(6):IF CUSPA6<0 THEN CUSPA6=CUSPA6+2#*PI

2660 K=(CUSPA6*18000/PI)/100:GOSUB 140

2670 QB6N$=QQB$

2680 VALA6=LLS(6)-LLS(7)

2690 CUSPA5=LLG-LLS(5):IF CUSPA5<0 THEN CUSPA5=CUSPA5+2#*PI

2700 K=(CUSPA5*18000/PI)/100:GOSUB 140

2710 QB5N$=QQB$

2720 VALA5= LLS(5)-LLS(6)

2730 CUSPA4=LLG-LLS(4):IF CUSPA4<0 THEN CUSPA4=CUSPA4+2#*PI

2740 K=(CUSPA4*18000/PI)/100:GOSUB 140

2750 QB4N$=QQB$

2760 VALA4= LLS(4)-LLS(5)

2770 CUSPA3=LLG-LLS(3):IF CUSPA3<0 THEN CUSPA3=CUSPA3+2#*PI

2780 K=(CUSPA3*18000/PI)/100:GOSUB 140

2790 QB3N$=QQB$

2800 VALA3= LLS(3)-LLS(4)

2810 CUSPA2=LLG-LLS(2):IF CUSPA2<0 THEN CUSPA2=CUSPA2+2#*PI

2820 K=(CUSPA2*18000/PI)/100:GOSUB 140

2830 QB2N$=QQB$

2840 VALA2= LLS(2)-LLS(3)

2850 CUSPA1=LLG:VALA1= 2*PI-LLS(2)

2860 K=(CUSPA1*18000/PI)/100:GOSUB 140

2870 QB1N$=QQB$

2880 IF D$="p" THEN 3640

2890 IF FF<0 THEN 3150

2900 PRINT #1,"Domification Régiomontanus hémisphère nord":PRINT"Domification Régiomontanus hémisphère nord"

2910 PRINT "Valeur de la maison 12 = ";FIX(VALA12*180000#/PI)/1000#;" et CUSPIDE12= ";FIX(CUSPA12*180000#/PI)/1000#;QB12N$

2920 PRINT #1," Valeur de la maison 12 = ";FIX(VALA12*180000#/PI)/1000#;" et CUSPIDE 12= ";FIX(CUSPA12*180000#/PI)/1000#;QB12N$

2930 PRINT " Valeur de la maison 11 = ";FIX(VALA11*180000#/PI)/1000#;" et CUSPIDE 11 = ";FIX(CUSPA11*180000#/PI)/1000#;QB11N$

2940 PRINT #1,"valeur de la maison 11 = ";FIX(VALA11*180000#/PI)/1000#;" et CUSPIDE 11 = ";FIX(CUSPA11*180000#/PI)/1000#;QB11N$

2950 PRINT "valeur de la maison 10 = ";FIX(VALA10*180000#/PI)/1000#;" et CUSPIDE10 (MC) = ";FIX(CUSPA10*180000#/PI)/1000#;QB10N$

2960 PRINT #1,"valeur de la maison 10 = ";FIX(VALA10*180000#/PI)/1000#;" et CUSPIDE 10 (MC) = ";FIX(CUSPA10*180000#/PI)/1000#;QB10N$

2970 PRINT "valeur de la maison 9 = ";FIX(VALA9*180000#/PI)/1000#;" et CUSPIDE 9= ";FIX(CUSPA9*180000#/PI)/1000#;QB9N$

2980 PRINT #1," Valeur de la maison 9 = ";FIX(VALA9*180000#/PI)/1000#;" et CUSPIDE 9 = ";FIX(CUSPA9*180000#/PI)/1000#;QB9N$

2990 PRINT " Valeur de la maison 8 = ";FIX(VALA8*180000#/PI)/1000#;" et CUSPIDE8 = ";FIX(CUSPA8*180000#/PI)/1000#;QB8N$

3000 PRINT #1,"Valeur de la maison 8 = ";FIX(VALA8*180000#/PI)/1000#;" et CUSPIDE 8 = ";FIX(CUSPA8*180000#/PI)/1000#;QB8N$

3010 PRINT " Valeur de la maison 7 = ";FIX(VALA7*180000#/PI)/1000#;" et CUSPIDE7 =(DESc)";FIX(CUSPA7*180000#/PI)/1000#;QB7N$

3020 PRINT #1," Valeur de la maison 7 = ";FIX(VALA7*180000#/PI)/1000#;" et CUSPIDE 7 (DESc) = ";FIX(CUSPA7*180000#/PI)/1000#;QB7N$

3030 PRINT " Valeur de la maison 6 = ";FIX(VALA6*180000#/PI)/1000#;" et CUSPIDE6 = ";FIX(CUSPA6*180000#/PI)/1000#;QB6N$

3040 PRINT #1," Valeur de la maison 6 = ";FIX(VALA6*180000#/PI)/1000#;" et CUSPIDE 6 = ";FIX(CUSPA6*180000#/PI)/1000#;QB6N$

3050 PRINT "valeur de la maison 5 = ";FIX(VALA5*180000#/PI)/1000#;" et CUSPIDE 5= ";FIX(CUSPA5*180000#/PI)/1000#;QB5N$

3060 PRINT #1,"valeur de la maison 5 = ";FIX(VALA5*180000#/PI)/1000#;" et CUSPIDE 5 = ";FIX(CUSPA5*180000#/PI)/1000#;QB5N$

3070 PRINT"valeur de la maison 4 = ";FIX(VALA4*180000#/PI)/1000#;" et CUSPIDE 4(FC) = ";FIX(CUSPA4*180000#/PI)/1000#;QB4N$

3080 PRINT #1,"valeur de la maison 4 = ";FIX(VALA4*180000#/PI)/1000#;" et CUSPIDE 4 (FC) = ";FIX(CUSPA4*180000#/PI)/1000#;QB4N$

3090 PRINT "valeur de la maison 3 = ";FIX(VALA3*180000#/PI)/1000#;" et CUSPIDE 3= ";FIX(CUSPA3*180000#/PI)/1000#;QB3N$

3100 PRINT #1," Valeur de la maison 3 = ";FIX(VALA3*180000#/PI)/1000#;" et CUSPIDE 3 = ";FIX(CUSPA3*180000#/PI)/1000#;QB3N$

3110 PRINT " Valeur de la maison 2 = ";FIX(VALA2*180000#/PI)/1000#;" et CUSPIDE2 = ";FIX(CUSPA2*180000#/PI)/1000#;QB2N$

3120 PRINT #1," Valeur de la maison 2 = ";FIX(VALA2*180000#/PI)/1000#;" et CUSPIDE 2 = ";FIX(CUSPA2*180000#/PI)/1000#;QB2N$

3130 PRINT "valeur de la maison 1 = ";FIX(VALA1*180000#/PI)/1000#;" et CUSPIDE 1(ASCENDANT) = ";FIX(LLG*180000#/PI)/1000#;QB1N$

3140 PRINT #1,"valeur de la maison 1 = ";FIX(VALA1*180000#/PI)/1000#;" et CUSPIDE 1 (ASCENDANT) = ";FIX(LLG*180000#/PI)/1000#;QB1N$:GOTO 3410

3150 CLGG=CLG*PI/180#:REM clg=llg+pi

3160 PRINT"Hémisphère sud":PRINT #1,"Hémisphère sud"

3170 PRINT "Valeur de la maison 12 = ";FIX(VALA12*180000#/PI)/1000#;" et CUSPIDE12= ";FIX(CUSPA6*180000#/PI)/1000#;QB6N$

3180 PRINT #1," Valeur de la maison 12 = ";FIX(VALA12*180000#/PI)/1000#;" et CUSPIDE 12= ";FIX(CUSPA6*180000#/PI)/1000#;QB6N$

3190 PRINT " Valeur de la maison 11 = ";FIX(VALA11*180000#/PI)/1000#;" et CUSPIDE 11 = ";FIX(CUSPA5*180000#/PI)/1000#;QB5N$

3200 PRINT #1,"valeur de la maison 11= ";FIX(VALA11*180000#/PI)/1000#;" et CUSPDE 11 = ";FIX(CUSPA5*180000#/PI)/1000#;QB5N$

3210 PRINT "valeur de la maison 10= ";FIX(VALA10*180000#/PI)/1000#;" et CUSPIDE10 (MC) = ";FIX(CUSPA4*180000#/PI)/1000#;QB4N$

3220 PRINT #1,"valeur de la maison 10= ";FIX(VALA10*180000#/PI)/1000#;" et CUSPIDE 10 (MC) = ";FIX(CUSPA4*180000#/PI)/1000#;QB4N$

3230 PRINT "valeur de la maison 9= ";FIX(VALA9*180000#/PI)/1000#;" et CUSPIDE 9= ";FIX(CUSPA3*180000#/PI)/1000#;QB3N$

3240 PRINT #1," Valeur de la maison 9= ";FIX(VALA9*180000#/PI)/1000#;" et CUSPIDE 9 = ";FIX(CUSPA3*180000#/PI)/1000#;QB3N$

3250 PRINT " Valeur de la maison 8= ";FIX(VALA8*180000#/PI)/1000#;" et CUSPIDE 8= ";FIX(CUSPA2*180000#/PI)/1000#;QB2N$

3260 PRINT #1,"Valeur de la maison 8= ";FIX(VALA8*180000#/PI)/1000#;" et CUSPIDE8 = ";FIX(CUSPA2*180000#/PI)/1000#;QB2N$

3270 PRINT " Valeur de la maison 7= ";FIX(VALA7*180000#/PI)/1000#;" et CUSPIDE 7=(DESc)";FIX(CUSPA1*180000#/PI)/1000#;QB1N$

3280 PRINT #1," Valeur de la maison 7= ";FIX(VALA7*180000#/PI)/1000#;" et CUSPIDE 7 (DESc) = ";FIX(CUSPA1*180000#/PI)/1000#;QB1N$

3290 PRINT " Valeur de la maison 6= ";FIX(VALA6*180000#/PI)/1000#;" et CUSPIDE 6= ";FIX(CUSPA12*180000#/PI)/1000#;QB12N$

3300 PRINT #1," Valeur de la maison 6 = ";FIX(VALA6*180000#/PI)/1000#;" et CUSPIDE 6 = ";FIX(CUSPA12*180000#/PI)/1000#;QB12N$

3310 PRINT "valeur de la maison 5 = ";FIX(VALA5*180000#/PI)/1000#;" et CUSPIDE 5= ";FIX(CUSPA11*180000#/PI)/1000#;QB11N$

3320 PRINT #1,"valeur de la maison 5 = ";FIX(VALA5*180000#/PI)/1000#;" et CUSPIDE 5 = ";FIX(CUSPA11*180000#/PI)/1000#;QB11N$

3330 PRINT"valeur de la maison 4 = ";FIX(VALA4*180000#/PI)/1000#;" et CUSPIDE 4(FC) = ";FIX(CUSPA10*180000#/PI)/1000#;QB10N$

3340 PRINT #1,"valeur de la maison 4 = ";FIX(VALA4*180000#/PI)/1000#;" et CUSPIDE 4 (FC) = ";FIX(CUSPA10*180000#/PI)/1000#;QB10N$

3350 PRINT "valeur de la maison 3 = ";FIX(VALA3*180000#/PI)/1000#;" et CUSPIDE 3= ";FIX(CUSPA9*180000#/PI)/1000#;QB9N$

3360 PRINT #1," Valeur de la maison 3 = ";FIX(VALA3*180000#/PI)/1000#;" et CUSPIDE 3 = ";FIX(CUSPA9*180000#/PI)/1000#;QB9N$

3370 PRINT " Valeur de la maison 2 = ";FIX(VALA2*180000#/PI)/1000#;" et CUSPIDE2 = ";FIX(CUSPA8*180000#/PI)/1000#;QB8N$

3380 PRINT #1," Valeur de la maison 2 = ";FIX(VALA2*180000#/PI)/1000#;" et CUSPIDE 2 = ";FIX(CUSPA8*180000#/PI)/1000#;QB8N$

3390 PRINT "valeur de la maison 1 = ";FIX(VALA1*180000#/PI)/1000#;" et CUSPIDE 1(ASCENDANT) = ";FIX(CLGG*180000#/PI)/1000#;QB7N$

3400 PRINT #1,"valeur de la maison 1 = ";FIX(VALA1*180000#/PI)/1000#;" et CUSPIDE 1 (ASCENDANT) = ";FIX(CLGG*180000#/PI)/1000#;QB7N$

3410 IF TT<PI/2# THEN 3440:REM gamma sur l'horizon

3420 IF TT>3#*PI/2# THEN 3440: REM gamma sur l'horizon

3430 GOTO 3530:REM gamma sous l'horizon

3440 PRINT "Les valeurs d'azimuts sont identiques HN et HS"

3450 PRINT #1,"Les valeurs d'azimuts sont identiques HN et HS"

3460 PRINT #1,"Azimut EST du Nonagésime = ";FIX((2#*PI-ABS(LT))*18000#/PI)/100#;"°"

3470 PRINT #1,"Hauteur du Nonagésime = ";FIX((PI/2#-LL)*18000#/PI)/100#;"°"

3480 PRINT #1,"Azimut du lever de l'écliptique = ";FIX((3#*PI/2#-ABS(LT))*18000#/PI)/100#

3490 PRINT #1,"Azimut du coucher de l'écliptique = ";FIX((PI/2-ABS(LT))*18000#/PI)/100#

3500 GOSUB 1250

3510 GOTO 3610

3520 REM gamma sous l'horizon

3530 PRINT "Les valeurs d'azimuts sont identiques HN et HS"

3540 PRINT #1,"Les valeurs d'azimuts sont identiques HN et HS"

3550 PRINT #1,"Azimut OUEST du Nonagésime = ";FIX(ABS(LT)*18000#/PI)/100#:REM gamma sous l'horizon.

3560 PRINT #1,"Hauteur du Nonagésime = ";FIX((PI/2#-LL)*18000#/PI)/100#;"°"

3570 PRINT #1,"Azimut du lever de l'écliptique = ";FIX((3#*PI/2#+ABS(LT))*18000#/PI)/100#

3580 PRINT #1,"Azimut du coucher de l'écliptique = ";FIX((PI/2#+ABS(LT))*18000#/PI)/100

3590 GOSUB 1250

3600 IF PLAREG=5 THEN 5190

3610 INPUT "Domification Placidus appuyer sur p; fin sur une autre lettre", P$

3620 IF P$ ="p" THEN 3640

3630 GOTO 5190

3640 PRINT" Domification Placidus": PRINT #1," Domification Placidus"

3650 ASDH=-TAN (-EP)*TAN(F):ASDH=ATN(SQR(1-ASDH^2)/ASDH):ASDE=-TAN(EP)*TAN(F):ASDE=ATN(SQR(1-ASDE^2)/ASDE) + PI

3660 REM Q devient Qa pour 2/3 asde et Qb pour 1/3 d'asde. De même pour Q1a et Q1b pour asdh

3670 REM on aura alors hQa et hQb, hQ1a et hQ1b. Les azimuts correspondants seront azQa, azQb et azQ1a et azQ1b

3680 TA=2*PI-2*ASDE/3:TB=2*PI-ASDE/3:T1A=2*PI-2*ASDH/3:T1B=2*PI-ASDH/3

3690 HQA=SIN(EP)*SIN(F)+COS(EP)*COS(F)*COS(TA):HQA=ATN(HQA/(SQR(1-HQA^2))):REM hQa <=> sin h puis sinus en fonction de la tangente de l'arc moitié

3700 HQB=SIN(EP)*SIN(F)+COS(EP)*COS(F)*COS(TB):HQB=ATN(HQB/(SQR(1-HQB^2)))

3710 HQ1A=SIN(-EP)*SIN(F)+COS(-EP)*COS(F)*COS(T1A):HQ1A=ATN(HQ1A/(SQR(1-HQ1A^2)))

3720 HQ1B=SIN(-EP)*SIN(F)+COS(-EP)*COS(F)*COS(T1B):HQ1B=ATN(HQ1B/(SQR(1-HQ1B^2)))

3730 AZQA=SIN(TA)/(SIN(F)*COS(TA)-COS(F)*TAN(EP)):AZQA=ATN(AZQA)

3740 IF AZQA >0 THEN AZQA=AZQA+PI:GOTO 3760

3750 : REM ici l'azimut est >pi voir l'étude lorsque l'azimut est compris entre pi et 2 pi

3760 AZQB=SIN(TB)/(SIN(F)*COS(TB)-COS(F)*TAN(EP)):AZQB=ATN(AZQB)

3770 IF AZQB >0 THEN AZQB=AZQB+PI:GOTO 3790

3780 IF AZQB <0 THEN AZQB=2*PI+AZQB

3790 AZQ1A=SIN(T1A)/(SIN(F)*COS(T1A)-COS(F)*TAN(-EP)):AZQ1A=ATN(AZQ1A)

3800 IF AZQ1A >0 THEN AZQ1A=AZQ1A+PI:GOTO 3820

3810 IF AZQ1A <0 THEN AZQ1A=2*PI+AZQ1A

3820 AZQ1B=SIN(T1B)/(SIN(F)*COS(T1B)-COS(F)*TAN(-EP)):AZQ1B=ATN(AZQ1B)

3830 IF AZQ1B >0 THEN AZQ1B=AZQ1B+PI:GOTO 3850

3840 IF AZQ1B <0 THEN AZQ1B=2*PI+AZQ1B

3850 DAZ1=AZQ1A-AZQA:DAZ2=AZQ1B-AZQB

3860 CS1=SIN(DAZ1)/((TAN(HQA)/TAN(HQ1A))-COS(DAZ1)):CS1=ATN(CS1): REM pour cuspide 12

3870 CS2= SIN(DAZ2)/((TAN(HQB)/TAN(HQ1B))-COS(DAZ2)):CS2=ATN(CS2): REM pour cuspide 11

3880 MT1= TAN(HQ1A)/SIN(CS1):MT1=ATN(MT1):REM mt1 est l'angle M de la maison XII

3890 MT2 = TAN(HQ1B)/SIN(CS2):MT2=ATN(MT2):REM mt2 est l'angle M de la maison XI

3900 SS1=2*PI-(AZQ1A+CS1):REM ss1 est SS' maison XII

3910 SS2=2*PI-(AZQ1B+CS2): LE=ABS(LT): REM ss2 = SS' maison XI LT est calcu3920 IF TT<=PI/2 THEN 3950

3930 IF TT>=3*PI/2 THEN 3950

3940 SL1=PI/2-(LE+SS1):SL2=PI/2-(LE+SS2):GOTO 3960:REM gamma sous l'horizon

3950 SL1=LE+PI/2-SS1:SL2=LE+PI/2-SS2:REM s1=S'L maison XII et sl2=S'L maison XI

gamma sur l'horizon

3960 JLP12=1 / (COS (LL) / (SIN (SL1)*TAN(MT1)) + SIN (LL)/TAN (SL1)):JLP12=ATN(
JLP12)
3965 IF JLP12<0 THEN JLP12=JLP12+PI
3967 MAS12=JLP12
3970 JLP11=1 / (COS (LL) / (SIN (SL2)*TAN(MT2)) + SIN (LL)/TAN (SL2)):JLP11=ATN(
JLP11)
3975 IF JLP11<0 THEN JLP11=JLP11+PI
3977 MAS11=JLP11-JLP12:MAS5=MAS11
3980 CUS10=LLG-LLS(10):IF CUS10<0 THEN CUS10=CUS10+2*PI
3990 JLP10=LLG-CUS10:IF JLP10<0 THEN JLP10=JLP10+2*PI

4000 CUS12=LLG-JLP12:IF CUS12<0 THEN CUS12 = CUS12+2*PI

4010 CUS11=LLG-JLP11:IF CUS11<0 THEN CUS11=CUS11+2*PI

4020 MAS10=JLP10-JLP11:MAS4=MAS10: REM les azimuts d'après-midi correspondent à 2pi-azimut du matin

4030 REM Les azimuts correspondent à 2 pi - azimut du matin

4040 AZQAW=2*PI-AZQA:AZQBW=2*PI-AZQB:AZQ1AW=2*PI-AZQ1A:AZQ1BW=2*PI-AZQ1B

4050 REM les différences des azimuts restent identiques au cas du matin. On obtient donc les mêmes valeurs pour M (mt1,2) et CS' (CS1,2)

4060 REM on garde également les mêmes valeurs SS' (ss1 et ss2) du matin car le matin SS' = 2pi-azQ1-CS' et l'après-midi SS'=azQ1-CS'. Les valeurs respectives de

4070 REM SS' sont égales et symétriques par rapport à la méridienne.

4080 REM par contre les valeurs de SL (SB l'après-midi; voir l'étude) vont devenir sl3 et sl4

4090 IF TT<=PI/2 THEN 4120

4100 IF TT>=3*PI/2 THEN 4120

4110 SL3=PI/2+LE-SS1:SL4=PI/2+LE-SS2:GOTO 4130:REM gamma sous l'horizon

4120 SL3=PI/2-(LE+SS1):SL4=PI/2-(LE+SS2):REM sl3=S'D en rapport avec la cuspid

e 8 et sl4=S'D en rapport avec la cuspide 9 gamma sur l'horizon

4130 JLP7=1 / (COS (LL) / (SIN (SL3)*TAN(MT1)) + SIN (LL)/TAN(SL3)):JLP7=ATN(JLP
7):IF JLP7<0 THEN JLP7=JLP7+PI
4135 CUS8=LLG+PI+JLP7:MAS7=JLP7:MAS1=MAS7:IF CUS8>2*PI THEN CUS8=CUS8-2*PI
4140 JLP8=1 / (COS (LL) / (SIN (SL4)*TAN(MT2)) + SIN (LL)/TAN (SL4)):JLP8=ATN(JL
P8):IF JLP8<0 THEN JLP8=JLP8+PI
4145 MAS8=JLP8-JLP7:CUS9=LLG+PI+JLP8:IF CUS9>2*PI THEN CUS9=CUS9-2*PI
4150 MAS9=CUS10-CUS9:IF MAS9<0 THEN MAS9=MAS9+2*PI

4160 MAS3=MAS9:CUS7=LLG+PI:IF CUS7>2*PI THEN CUS7=CUS7-2*PI:REM cus7=descendant

4170 MAS2=MAS8

4180 MAS6=MAS12:REM ici en radians voir l'étude pour l'égalité des maisons

4190 CUS6=CUS7-MAS6:IF CUS6<0 THEN CUS 6=CUS6+2*PI

4200 CUS5=CUS7-(MAS6+MAS5):IF CUS5<0 THEN CUS5=CUS5+2*PI

4210 CUS4=CUS7-(MAS6+MAS5+MAS4): IF CUS4<0 THEN CUS4=CUS4+2*PI

4220 CUS3=LLG+MAS1+MAS2: IF CUS3>2*PI THEN CUS3=CUS3-2*PI

4230 CUS2=LLG+MAS1: IF CUS2>2*PI THEN CUS2=CUS2-2*PI

4240 CUS1=LLG: MAS12=MAS12*180/PI:MAS11=MAS11*180/PI:MAS10=MAS10*180/PI:MAS9=MAS

9*180/PI:MAS8=MAS8*180/PI:MAS7=MAS7*180/PI

4250 MAS6=MAS12:MAS5=MAS11:MAS4=MAS10:MAS3=MAS9:MAS2=MAS8:MAS1=MAS7:REM mas6=mas12 ....mas1=mas7 ici en degrès voir l'étude

4260 PRINT"ooooooooooooooooooooooooooooooooooooo":PRINT #1,"ooooooooooooooooooooooooooooooooooooo"

4270 PRINT"Domification Placidus hémisphère nord":PRINT# 1,"Domification Placidus hémisphère nord"

4280 REM cuspide 1 et maison 1

4290 KCUS1=CUS1*180/PI:I=INT(KCUS1/30):PCUS1=INT((KCUS1-INT(KCUS1))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4300 K=KCUS1:GOSUB 140

4310 PRINT"Position de la cuspide 1 = ";INT(KCUS1);"°";PCUS1;"'";QQB$;" Valeur de la maison 1 = "; INT(MAS1*1000)/1000;"°"

4320 PRINT #1,"Position de la cuspide 1 = ";INT(KCUS1);"°";PCUS1;"'";QQB$;" Valeur de la maison 1 = "; INT(MAS1*1000)/1000;"°":Q1N$=QQB$

4330 REM cuspide 2 et maison 2

4340 KCUS2=CUS2*180/PI:I=INT(KCUS2/30):PCUS2=INT((KCUS2-INT(KCUS2))*6000)/100

4350 K=KCUS2:GOSUB 140

4360 PRINT"Position de la cuspide 2 = ";INT(KCUS2);"°";PCUS2;"'";QQB$;" Valeur de la maison 2 = "; INT(MAS2*1000)/1000;"°"

4370 PRINT #1,"Position de la cuspide 2 = ";INT(KCUS2);"°";PCUS2;"'";QQB$;" Valeur de la maison 2 = "; INT(MAS2*1000)/1000;"°":Q2N$=QQB$

4380 REM cuspide 3 et maison 3

4390 KCUS3=CUS3*180/PI:I=INT(KCUS3/30):PCUS3=INT((KCUS3-INT(KCUS3))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4400 K=KCUS3:GOSUB 140

4410 PRINT"Position de la cuspide 3 = ";INT(KCUS3);"°";PCUS3;"'";QQB$;" Valeur de la maison 3 = "; INT(MAS3*1000)/1000;"°"

4420 PRINT #1,"Position de la cuspide 3 = ";INT(KCUS3);"°";PCUS3;"'";QQB$;" Valur de la maison 3 = "; INT(MAS3*1000)/1000;"°":Q3N$=QQB$

4430 REM cuspide 4 et maison 4

4440 KCUS4=CUS4*180/PI:I=INT(KCUS4/30):PCUS4=INT((KCUS4-INT(KCUS4))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4450 K=KCUS4:GOSUB 140

4460 PRINT"Position de la cuspide 4 = ";INT(KCUS4);"°";PCUS4;"'";QQB$;" Valeur de la maison 4 = "; INT(MAS4*1000)/1000;"°"

4470 PRINT #1,"Position de la cuspide 4 = ";INT(KCUS4);"°";PCUS4;"'";QQB$;" Valeur de la maison 4 = "; INT(MAS4*1000)/1000;"°":Q4N$=QQB$

4480 REM cuspide 5 maison 5

4490 KCUS5=CUS5*180/PI:I=INT(KCUS5/30):PCUS5=INT((KCUS5-INT(KCUS5))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4500 K=KCUS5:GOSUB 140

4510 PRINT"Position de la cuspide 5 = ";INT(KCUS5);"°";PCUS5;"'";QQB$;" Valeur de la maison 5 = "; INT(MAS5*1000)/1000;"°"

4520 PRINT #1,"Position de la cuspide 5 = ";INT(KCUS5);"°";PCUS5;"'";QQB$;" Valeur de la maison 5 = "; INT(MAS5*1000)/1000;"°":Q5N$=QQB$

4530 REM cuspide 6 maison 6

4540 KCUS6=CUS6*180/PI:I=INT(KCUS6/30):PCUS6=INT((KCUS6-INT(KCUS6))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4550 K=KCUS6:GOSUB 140

4560 PRINT"Position de la cuspide 6 = ";INT(KCUS6);"°";PCUS;"'";QQB$;" Valeur dela maison 6 = "; INT(MAS6*1000)/1000;"°"

4570 PRINT #1,"Position de la cuspide 6 = ";INT(KCUS6);"°";PCUS6;"'";QQB$;" Valeur de la maison 6 = "; INT(MAS6*1000)/1000;"°":Q6N$=QQB$

4580 REM cuspide 7 maison 7

4590 KCUS7=CUS7*180/PI:I=INT(KCUS7/30):PCUS7=INT((KCUS7-INT(KCUS7))*6000)/100:REM pcus partie décimale de kcus transformée en ' d'angle

4600 K=KCUS7:GOSUB 140

4610 PRINT"Position de la cuspide 7 = ";INT(KCUS7);"°";PCUS7;"'";QQB$;" Valeur de la maison 7 = "; INT(MAS7*1000)/1000;"°"

4620 PRINT #1,"Position de la cuspide 7 = ";INT(KCUS7);"°";PCUS7;"'";QQB$;" Valeur de la maison 7 = "; INT(MAS7*1000)/1000;"°":Q7N$=QQB$

4630 REM cuspide 8 maison 8

4640 KCUS8=CUS8*180/PI:I=INT(KCUS8/30):PCUS8=INT((KCUS8-INT(KCUS8))*6000)/100

4650 K=KCUS8:GOSUB 140

4660 PRINT"Position de la cuspide 8 = ";INT(KCUS8);"°";PCUS8;"'";QQB$;" Valeur de la maison 8 = "; INT(MAS8*1000)/1000;"°"

4670 PRINT #1,"Position de la cuspide 8 = ";INT(KCUS8);"°";PCUS8;"'";QQB$;" Valeur de la maison 8 = "; INT(MAS8*1000)/1000;"°":Q8N$=QQB$

4680 REM cuspide 9 maison 9

4690 KCUS9=CUS9*180/PI:I=INT(KCUS9/30):PCUS9=INT((KCUS9-INT(KCUS9))*6000)/100

4700 K=KCUS9:GOSUB 140

4710 PRINT"Position de la cuspide 9 = ";INT(KCUS9);"°";PCUS9;"'";QQB$;" Valeur de la maison 9 = "; INT(MAS9*1000)/1000;"°"

4720 PRINT #1,"Position de la cuspide 9 = ";INT(KCUS9);"°";PCUS9;"'";QQB$;" Valeur de la maison 9 = "; INT(MAS9*1000)/1000;"°":Q9N$=QQB$

4730 REM cuspide 10 maison 10

4740 KCUS10=CUS10*180/PI:I=INT(KCUS10/30):PCUS10=INT((KCUS10-INT(KCUS10))*6000)/100

4750 K=KCUS10:GOSUB 140

4760 PRINT"Position de la cuspide 10 = ";INT(KCUS10);"°";PCUS10;"'";QQB$;" Valeur de la maison 10 = "; INT(MAS10*1000)/1000;"°"

4770 PRINT #1,"Position de la cuspide 10 = ";INT(KCUS10);"°";PCUS10;"'";QQB$;" Valeur de la maison 10 = "; INT(MAS10*1000)/1000;"°":Q10N$=QQB$

4780 REM cuspide 11 et maison 11

4790 KCUS11=CUS11*180/PI:I=INT(KCUS11/30):PCUS11=INT((KCUS11-INT(KCUS11))*6000)/100

4800 K=KCUS11:GOSUB 140

4810 PRINT"Position de la cuspide 11 = ";INT(KCUS11);"°";PCUS11;"'";QQB$;" Valeur de la maison 11 = "; INT(MAS11*1000)/1000;"°"

4820 PRINT #1,"Position de la cuspide 11 = ";INT(KCUS11);"°";PCUS11;"'";QQB$;" Valeur de la maison 11 = "; INT(MAS11*1000)/1000;"°":Q11N$=QQB$

4830 REM cuspide 12 et maison 12

4840 KCUS12=CUS12*180/PI:I=INT(KCUS12/30):PCUS12=INT((KCUS12-INT(KCUS12))*6000)/100

4850 K=KCUS12:GOSUB 140

4860 PRINT"Position de la cuspide 12 = ";INT(KCUS12);"°";PCUS12;"'";QQB$;" Valeur de la maison 12 = "; INT(MAS12*1000)/1000;"°"

4870 PRINT #1,"Position de la cuspide 12 = ";INT(KCUS12);"°";PCUS12;"'";QQB$;" Valeur de la maison 12 = "; INT(MAS12*1000)/1000;"°":Q12N$=QQB$

4880 INPUT "Domification de l'hémisphère sud? appuyez sur s. Pour terminer appuyez sur une autre lettre",U$

4890 IF U$<>"s" THEN 5220

4900 PRINT"Un temps sidéral TS nord correspond au même instant au temps sidéral TS + 12 sud.

Le programme réappareille les numéros de maisons pour la domification sud."

4910 REM On a M12=M6....seules les cuspides changent de nom: cuspide 7 nord devient cuspide 1 sud...

4920 PRINT"Domification Placidus hémisphère sud":PRINT #1,"oooooooooooooooooooooooooooooooooooo"

4930 PRINT #1,"Domification Placidus hémisphère sud"

4940 PRINT"Position de la cuspide 12 = ";INT(KCUS6);"°";INT(PCUS6*100)/100;"'";Q6N$;" Valeur de la maison 12 = "; INT(MAS6*1000)/1000;"°"

4950 PRINT #1,"Position de la cuspide 12 = ";INT(KCUS6);"°";INT(PCUS6*100)/100;"'";Q6N$;" Valeur de la maison 12 = "; INT(MAS6*1000)/1000;"°"

4960 PRINT"Position de la cuspide 11 = ";INT(KCUS5);"°";INT(PCUS5*100)/100;"'";Q5N$;" Valeur de la maison 11 = "; INT(MAS5*1000)/1000;"°"

4970 PRINT #1,"Position de la cuspide 11 = ";INT(KCUS5);"°";INT(PCUS5*100)/100;"'";Q5N$;" Valeur de la maison 11 = "; INT(MAS5*1000)/1000;"°"

4980 PRINT #1,"Position de la cuspide 10 = ";INT(KCUS4);"°";INT(PCUS4*100)/100;"'";Q4N$;" Valeur de la maison 10 = "; INT(MAS4*1000)/1000;"°"

4990 PRINT "Position de la cuspide 10 = ";INT(KCUS4);"°";INT(PCUS4*100)/100;"'";Q4N$;" Valeur de la maison 10 = "; INT(MAS4*1000)/1000;"°"

5000 PRINT #1,"Position de la cuspide 9 = ";INT(KCUS3);"°";INT(PCUS3*100)/100;"'";Q3N$;" Valeur de la maison 9 = "; INT(MAS3*1000)/1000;"°"

5010 PRINT "Position de la cuspide 9 = ";INT(KCUS3);"°";INT(PCUS3*100)/100;"'";Q3N$;" Valeur de la maison 9 = "; INT(MAS3*1000)/1000;"°"

5020 PRINT #1,"Position de la cuspide 8 = ";INT(KCUS2);"°";INT(PCUS2*100)/100;"'";Q2N$;" Valeur de la maison 8 = "; INT(MAS2*1000)/1000;"°"

5030 PRINT "Position de la cuspide 8 = ";INT(KCUS2);"°";INT(PCUS2*100)/100;"'";Q2N$;" Valeur de la maison 8 = "; INT(MAS2*1000)/1000;"°"

5040 PRINT #1,"Position de la cuspide 7 = ";INT(KCUS1);"°";INT(PCUS1*100)/100;"'";Q1N$;" Valeur de la maison 7 = "; INT(MAS1*1000)/1000;"°"

5050 PRINT "Position de la cuspide 7 = ";INT(KCUS1);"°";INT(PCUS1*100)/100;"'";Q1N$;" Valeur de la maison 7 = "; INT(MAS1*1000)/1000;"°"

5060 PRINT"Position de la cuspide 6 = ";INT(KCUS12);"°";INT(PCUS12*100)/100;"'";Q12N$;" Valeur de la maison 6 = "; INT(MAS12*1000)/1000;"°"

-5070 PRINT #1,"Position de la cuspide 6 = ";INT(KCUS12);"°";INT(PCUS12*100)/100;"'";Q12N$;" Valeur de la maison 6 = "; INT(MAS12*1000)/1000;"°"

5080 PRINT"Position de la cuspide 5 = ";INT(KCUS11);"°";INT(PCUS11*100)/100;"'";Q11N$;" Valeur de la maison 5 = "; INT(MAS11*1000)/1000;"°"

5090 PRINT #1,"Position de la cuspide 5 = ";INT(KCUS11);"°";INT(PCUS11*100)/100;"'";Q11N$;" Valeur de la maison 5 = "; INT(MAS11*1000)/1000;"°"

5100 PRINT"Position de la cuspide 4 = ";INT(KCUS10);"°";INT(PCUS10*100)/100;"'";Q10N$;" Valeur de la maison 4 = "; INT(MAS10*1000)/1000;"°"

5110 PRINT #1,"Position de la cuspide 4 = ";INT(KCUS10);"°";INT(PCUS10*100)/100;"'";Q10N$;" Valeur de la maison 4 = "; INT(MAS10*1000)/1000;"°"

5120 PRINT"Position de la cuspide 3 = ";INT(KCUS9);"°";INT(PCUS9*100)/100;"'";Q9N$;" Valeur de la maison 3 = "; INT(MAS9*1000)/1000;"°"

5130 PRINT #1,"Position de la cuspide 3 = ";INT(KCUS9);"°";INT(PCUS9*100)/100;"'";Q9N$;" Valeur de la maison 3 = "; INT(MAS9*1000)/1000;"°"

5140 PRINT"Position de la cuspide 2 = ";INT(KCUS8);"°";INT(PCUS8*100)/100;"'";Q8N$;" Valeur de la maison 2 = "; INT(MAS8*1000)/1000;"°"

5150 PRINT #1,"Position de la cuspide 2 = ";INT(KCUS8);"°";INT(PCUS8*100)/100;"'";Q8N$;" Valeur de la maison 2 = "; INT(MAS8*1000)/1000;"°"

5160 PRINT"Position de la cuspide 1 = ";INT(KCUS7);"°";INT(PCUS7*100)/100;"'";Q7N$;" Valeur de la maison 1 = "; INT(MAS7*1000)/1000;"°"

5170 PRINT #1,"Position de la cuspide 1 = ";INT(KCUS7);"°";INT(PCUS7*100)/100;"'";Q7N$;" Valeur de la maison 1 = "; INT(MAS7*1000)/1000;"°"

5180 PLAREG=5:GOTO 3410

5190 INPUT"nouveau TS appuyer sur n; fin sur f",KT$

5200 IF KT$="f" THEN 5220

5210 GOTO 390

5220 CLOSE

5230 END

5 3 2016            mise à jour le 27 1 2023

Retour à "Mes travaux personnels"

Cadrans solaires Pakhomoff

haut de page