Intersection des
cercles horaires et verticaux
application aux cadrans solaires
Jean Pakhomoff
Nous calculons l'arc de vertical ZM compris entre le zénith et l'intersection de ce vertical avec un cercle horaire sur l'arc semi-diurne de l'astre M puis l'angle horaire t correspondant à cette intersection.
Ces résultats nous serviront par la suite
pour connaître l'heure d'apparition et de disparition du soleil
sur un cadran solaire vertical déclinant.
Nous nous sommes limités à l'hémisphère
nord. Il conviendra de faire un travail d'adaptation pour
l'hémisphère sud.

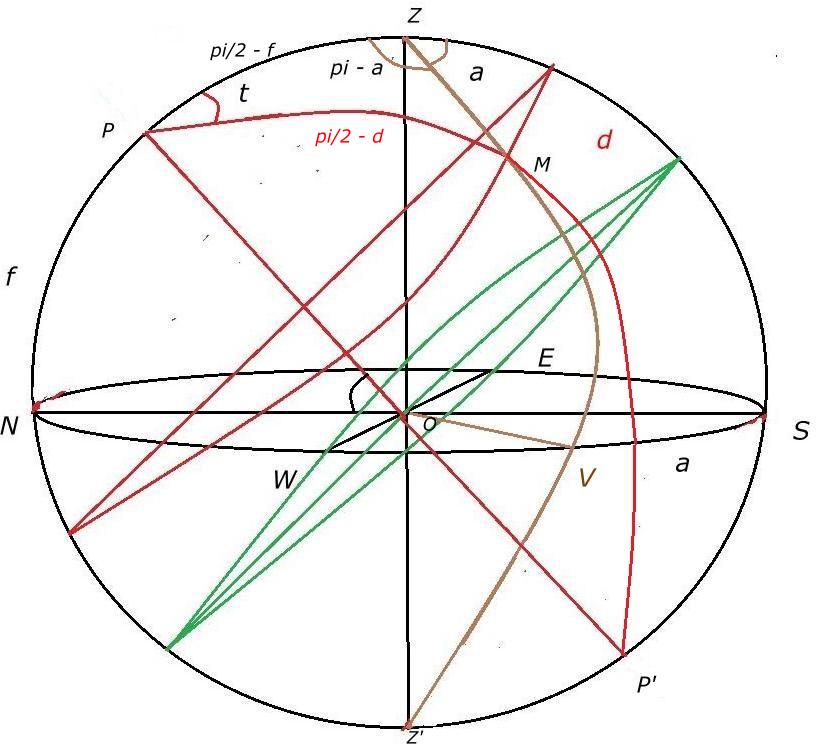
fig 1
Soit donc P le pôle nord, Z le zénith, PP' l'axe polaire faisant avec l'horizon un angle f égal à la latitude, ZZ' l'axe zénith nadir,
NESW les 4 points cardinaux, a l'azimut de M et t son angle horaire. PMP' est l'hémi cercle horaire passant par M et
ZVZ' l'hémi cercle d'azimut.
M sur son arc semi-diurne à l'intersection
de PMP' et de ZVZ'. La déclinaison de M est d.
ZM est le complément de la hauteur de
l'astre M sur l'horizon.
a et t varient de 0 à 2 pi à partir du
méridien sud d'ouest en est.
On appellera asd l'arc semi-diurne de
l'astre M.
Autrement dit la moitié NZSZ'W de la sphère céleste correspond aux heures d'après midi pm et la moitié NZSZ'E correspond aux heures
du matin am.
Dans le triangle paralactique PZM on PZ =
pi/2 – f, PM = pi/2 – d,
PZM = pi – a. Nous
appellerons M l'angle PMZ.
Calcul de M
On peut écrire sin (pi/2 – f) / sin M
= sin (pi/2 – d) / sin (pi – a)
et sin M = cos f sin a / cos d
(1)
Remarquons que M reste inférieur ou
égal à pi/2 tant que les arcs diurnes culminent sous le zénith
(d < f).
Nous en donnerons une démonstration
ci-dessous à propos
de la relation (2')
Lorsque M = pi / 2 alors sin M = 1 et cos d
= cos f sin a
Ceci n'est vérifié qu'à l'équateur
lorsque a = pi/2 et d = f = 0
Si la culmination a lieu au-delà du zénith, vers le nord, l'arc semi-diurne est alors coupé deux fois par le vertical et on a
deux valeurs de M données par le sinus .
L'une inférieure à pi/2, l'autre supérieure égale à pi - M.
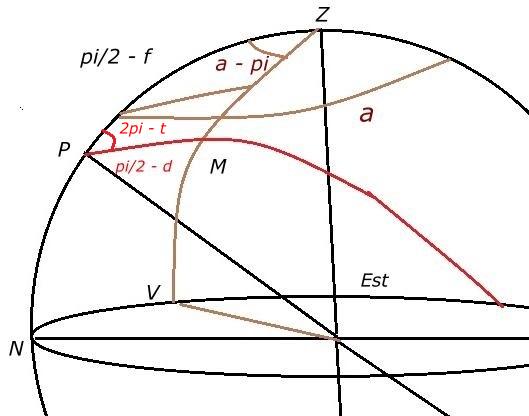
Remarquons également que lorsque a > pi alors la calculette donne la valeur négative de M. Pour n'avoir que sa valeur positive
on prend dans le triangle PZM du secteur am
de la sphère céleste la valeur PZM = a – pi.
On peut cependant garder en am pour M la valeur <0 fournie par l'ordinateur car cela ne change pas la valeur de ZM où
M intervient par son cosinus (cos M = cos
(-M) )
cos (pi/2 – f) = cos (pi/2 – d)
cos ZM + sin (pi/2 – d) sin ZM cos M
sin f = sin d cos ZM + cos d sin ZM cos M
(2)
Remarquons ici que de (2) on tire
cos M = (sin f – sin d cos ZM)
/ cos d sin ZM (2')
cos d est > 0 que d soit < 0 ou >
0. ZM < pi donc sin ZM > 0
sin f > 0 et d < f quand la culmination a lieu entre le zénith et le cardinal sud. Donc sin d < sin f et sin d cos ZM sera
une quantité > 0 ou < 0 inférieure à sin f en valeur absolue. Elle s'ajoutera à sa valeur si < 0 ou s'y soustraira si > 0.
cos M est donc toujours > 0 et M <
pi/2.
Nous verrons qu'il n'en est plus de même
lorsque d > f (la culmination se faisant alors entre le
zénith et le cardinal nord).
cos (pi/2 – d) = cos (pi/2 – f)
cos ZM + sin (pi/2 – f) sin ZM cos (pi – a)
sin d = sin f cos ZM + cos f sin ZM cos (pi
– a)
On remarque que cos (pi – a) = cos (a
– pi) = - cos a donc la relation est identique en pm et en
am et on peut écrire:
sin d = sin f cos ZM – cos f sin ZM
cos a (3)
De (2) on tire cos ZM = (sin f –
cos d sin ZM cos M) / sin d
et en remplaçant cos ZM par sa valeur dans
(3)
sin d = sin f ((sin f – cos d sin ZM
cos M) / sin d) - cos f sin ZM cos a
ce qui donne après développement
(4)
sin ZM = (sin²f – sin² d) / (cos d
cos M sin f + sin d cos f cos a)
ZM est donné par son sinus et celui-ci
renverra à deux valeurs de ZM: ZM et pi – ZM
Remarque: M ne prend qu'une valeur (> 0) lorsque d < f (astre culminant avant le zénith dans la zone sud de la sphère céleste).
On peut donc retenir les valeurs ZM et pi – ZM car ces valeurs sont rattachées à une seule valeur de M.
Ceci n'est plus vrai comme nous le verrons
plus bas lorsque d > f quand la culmination se fait entre le
pôle et le zénith.
Ne connaissant pas à cet instant la valeur
de t on ne peut savoir si
ZM est > ou < pi/2 autrement dit si
l'astre est sur ou sous l'horizon.
ZM = pi/2 lors des levers ou couchers.
Ici nous connaissons d et f et la relation (3)
devient lorsque ZM = pi/2
sin d = sin f cos ZM + cos f sin ZM cos (pi
– a) pm
cos (pi – a) = sin d / cos f
et ac = pi - arc cos (pi – a)
ac étant l'azimut du coucher
sin d = cos f cos (pi – a) = - cos f
cos a
sin d = sin f cos ZM + cos f sin ZM cos (a -
pi) am
cos ( a – pi) = sin d / cos f
et al = arc cos (a – pi) + pi
al étant l'azimut du lever
sin d = cos f cos (a - pi) = - cos f cos a
d est la déclinaison d'un astre se couchant
ou se levant dans l'azimut a sur un horizon de latitude f.
Donc même relation en ce qui concerne sin d
pour am et pm
Lorsqu'on prend pour azimut l'azimut ag (comme azimut gnomonique) d'un cadran solaire en tenant compte de sa déclinaison
gnomonique comme nous le verrons plus loin on peut trouver la déclinaison correspondante pour laquelle ZM = pi/2 c'est-à-dire
que le lever ou le coucher a lieu dans le
vertical du cadran.
On appellera cette valeur
particulière de la déclinaison dm:
sin dm = - cos f cos ag
Pour toute déclinaison inférieure le soleil se lèvera ou se couchera devant le cadran vers le sud et l'intersection vertical cercle horaire
aura lieu sous l'horizon entraînant ZM >
pi/2.
Les déclinaisons supérieures correspondront à un lever ou un coucher derrière le cadran vers le nord et l'intersection vertical cercle horaire
aura lieu au-dessus de l'horizon.
Remarquons encore que l'azimut du lever ou du coucher d'un astre de déclinaison d sur un horizon de latitude f se déduit comme
nous venons de le voir de la relation (3):
ZM étant égal à pi/2 on a
sin d =– cos f cos a (3')
Pour éviter les erreurs sur la valeur de l'arc
sinus a il vaut mieux employer la relation (3) quand Z =
pi/2 sous ses deux formes:
cos (pi – ac) = sin d / cos f
en pm
cos ( al – pi) = sin d / cos f
en am
Si ag > al alors ZM < pi/2: le lever
se fait depuis l' arrière du vertical vers le nord et
l'intersection a lieu sur l'horizon dans la zone Est (am).
Si ag > ac alors ZM > pi/2: le coucher
se fait en avant du vertical et l'intersection a lieu sous
l'horizon dans la zone Ouest (pm).
Si ag < al alors ZM > pi/2: le lever
se fait en avant du vertical vers le sud et l'intersection a lieu
sous l'horizon dans la zone Est (am).
Si ag < ac alors ZM < pi/2: le coucher
se fait en arrière du vertical et l'intersection a lieu sur
l'horizon dans la zone Ouest (pm).
Détermination de t correspondant à
cette intersection
On peut écrire de même
cos ZM = cos (pi/2 – f) cos (pi/2
– d) + sin (pi/2 – f) sin (pi/2 – d) cos t
Dans la zone am on a cos (2pi – t)
et cos (2pi – t) = cos t
donc même relation
et cos t = (cos ZM – sin f sin d) /
cos f cos d (5)
On a également sin t / sin ZM = sin (pi
– a) / sin (pi/2 – d)
et sin t = sin a sin ZM / cos d
zone pm
en zone am sin (2pi –
t) / sin ZM = sin (a – pi) / sin (pi/2 – d)
- sin t / sin ZM = - sin a / cos d
sin t = sin a sin ZM / cos d
(6)
même relation que zone pm
t varie de 0 à 2 pi
On recherchera cependant par commodité t
par son cosinus.
Entre 0 et pi le cosinus est > 0 si t
< pi/2 et < 0 si t > pi/2. La calculette fournit
directement la valeur positive de t entre 0 et pi.
Si t > pi, a est > pi et le
cosinus est < 0 jusqu'à 3 pi/2 puis positif jusqu'à 2 pi.
Donc si a > pi et cosinus t < 0 on prend la valeur 2pi - t
la calculette fournissant l'angle le plus petit ayant même cosinus, par exemple cos 250 = -.342020 arc cosinus = 110, il faut prendre
360 – 110 = 250.
si a > pi et cos t positif t est alors compris entre 3pi/2 et 2pi. La calculette donne également l'angle positif le plus petit et on prendra
pareillement pour t la valeur 2pi – t.