 fig
1
fig
1
Construction du cadran solaire horizontal
à partir des cercles horaires
par
Jean Pakhomoff
On connaît la méthode habituelle qui repose sur la connaissance de la hauteur du soleil et de son azimut pour tracer les lignes horaires
et les arcs diurnes sur le cadran horizontal.
 fig
1
fig
1
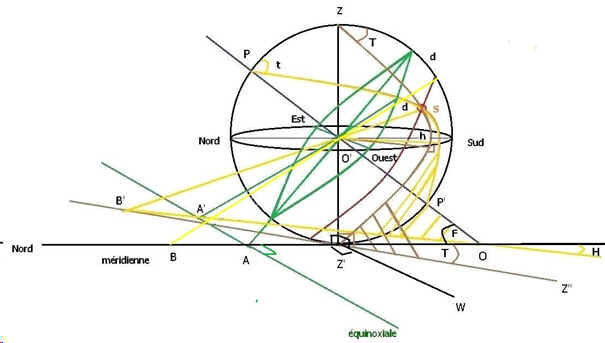
La figure 1 montre une sphère céleste de centre O' avec un grand cercle horizon de latitude F. L'axe des pôles perce en 0 un plan horizontal parallèle au cercle horizon.
L'axe ZZ' zénith nadir donne le grand cercle vertical ZSZ' passant par le soleil S. Ce vertical détermine l'azimut T avec le plan méridien.
Ce grand cercle coupe le plan horizontal perpendiculairement donnant la ligne Z'Z'' et l'angle OZ'Z'' est l'azimut du soleil.
L'axe PP' axe de rotation passant par les pôles PP' donne naissance au grand cercle horaire PSP' coupant le plan horizontal selon la ligne horaire tabulaire
OB' donnant l'angle horaire tabulaire H.
Sur ce grand cercle horaire le soleil S est représenté sur un petit cercle de déclinaison d. L'intersection du vertical et du cercle horaire passant par S
correspond au rayon de soleil passant par O' et venant percer le plan horizontal OZ'W en B'.
Ce rayon étant commun aux deux cercles ci-dessus il passe donc par l'intersection de leurs traces sur le plan OZ'W.
La figure 2 montre cela avec plus de précision:
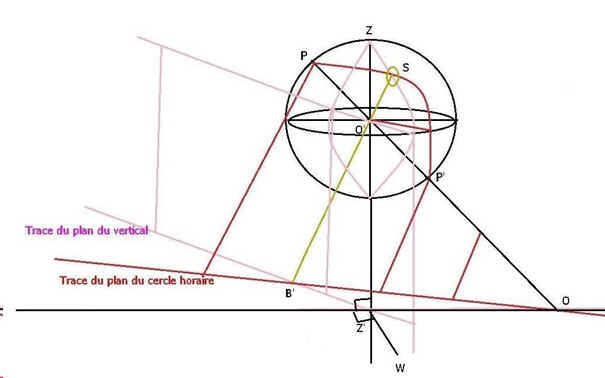 fig 2
fig 2
On fait glisser l'horizon le long de l'axe zénith nadir. On obtient le plan OZ'W qui est celui d'un cadran horizontal.
On prolonge le plan du cercle grand vertical passant par S et ayant l'axe zénith nadir pour diamètre.
De même on prolonge le plan du cercle horaire passant par S et ayant pour diamètre l'axe des pôles PP'.
Les traces de ces deux plans sur le plan horizontal se coupent en B' et le rayon solaire SO' étant commun au vertical et au
cercle horaire passe par B'.
Le grand cercle de l'équateur perpendiculaire à l'axe de rotation PP' est représenté en vert (fig 1).
Son plan coupe le plan horizontal selon l'équinoxiale perpendiculaire à la méridienne.
Le grand cercle méridien PZP' donne la méridienne Z'O.
La hauteur h de S se compte sur le grand vertical passant par S et la déclinaison d sur le cercle horaire.
La calcul de la hauteur h du soleil déclinant de d et de son azimut T pour l'angle horaire t à la latitude F permet alors facilement de connaître
l'angle tabulaire H et les coordonnées x et y du point B' et donc de tracer l'arc diurne pour cette déclinaison.
Une autre méthode de construction permet de se passer de la connaissance de la hauteur et de l'azimut.
L'observation de la figure 1 permet de constater que la ligne de midi en provenance de l'équateur coupe sur le cadran la méridienne en A.
Le rayon du soleil S de déclinaison d passant au méridien coupe la méridienne en B.
Un temps t plus tard le soleil étant en S sur son grand cercle horaire t et sur son petit cercle de déclinaison d la ligne horaire correspondant
à t en provenance de l'équateur coupe l'équatoriale en A' sur le cadran et le rayon de soleil SO' perce le cadran en B' sur la ligne horaire
tabulaire H correspondnt à t.
On constate que les angles AO'B et A'O'B' sont égaux car représentant la déclinaison d considérée constante pour les quelques heures de
parcours de l'arc diurne.
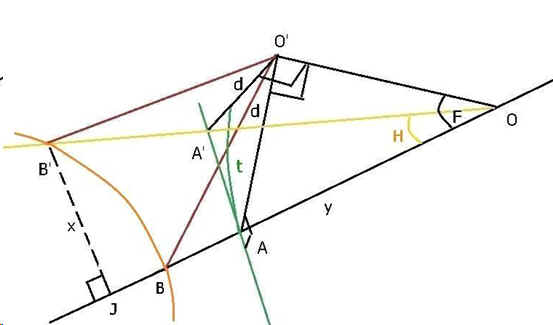 fig 3
fig 3
La figure 3 plus aérée montre cela plus facilement.
AA'O' étant le plan de l'équateur céleste l'angle d de déclinaison étant constant la longueur du rayon va être plus ou moins longue
selon l'angle horaire t. La détermination des différentes longueur de O'B' et de AA' en fonction de t va permettre de tracer et la ligne
horaire tabulaire et l'arc diurne correspondant à d.
On pose OO' = l latitude = F déclinaison = d
O'A' cos t = O'A = l tg F ==> O'A' = l tg F / cos t
O'A' sin t = AA' = (l tg F / cos t) sin t = l tg F tg t
O'ÔA' <=> O'ÔB' ==> O'A' / OO' = tg O'ÔB' = (l tg F / cos t) / l = tg F / cos t
On connaît alors O'ÔB' <=> O'ÔA'
Dans le triangle O'B'O on a O'B'O = p- (p / 2 + d + O'ÔB') = p / 2 – (d + O'ÔB')
sin O'B'O / l = sin (p / 2 + d) / OB' et OB' = l cos d / sin O'B'O
sin O'ÔB' / O'B' = sin (p / 2 + d) / OB' et O'B' = sin O'ÔB' . OB' / cos d
Dans le triangle O'BO on a O'BO = p – (p / 2 + d + F) = p / 2 – (d + F)
Dans le triangle O'AB on a O'AB = p – (p / 2 – F) = p / 2 + F
sin (p / 2 – (d + F)) / O'A = sin d / AB O'A = l tg F et AB = l tg F sin d / cos (F + d)
Dans le triangle O'OA' on a O'A'O = p – (p / 2 + O'ÔB') = p / 2 –O'ÔB')
d'où O'A'B' = p – (p / 2 – O'ÔB')) = p / 2 + O'ÔB'
et le triangle O'A'B' permet d'écrire
sin d / A'B' = sin (p / 2 + O'ÔB') / O'B' et A'B' = O'B' sin d / cos O'ÔB'
On retrouve la formule classique donnant l'angle tabulaire du cadran horizontal:
dans le triangle OA'A on peut écrire A'A / OA = tg H = l tg F tg t / (l / cos F)
tg H = l tg F tg t cos F / l et tg H = sin F tg t
Le point B' de l'arc diurne est alors connu par la quantité OB' portée sur la ligne horaire H.
En projetant B' en J sur la méridienne on obtient les coordonnées rectangulaires de B':
B'J = x = OB' sin H
OJ = y = OB' cos H
Remarque:
Les formules ci-dessus ont été établies dans le cas des déclinaisons négatives.
Pour les déclinaisons positives les arcs diurnes se trouvent entre l'équinoxiale et l'axe pôlaire. on obtient:
O'B'O = p / 2 – (O'ÔB' - d)
OB' = l cos d / sin O'B'O sans changement
O'B' = sin O'ÔB' . OB' / cos d sans changement
AB = l tg F sin d / cos (F - d)
A'B' = O'B' sin d / cos O'ÔB' sans changement
On entrera la valeur absolue de d pour le calcul.
Le reste des formules est sans changement.
Le 12 9 2014


Cadran horizontal tracé à partir
du plan équatorial
Retour à "mes travaux en gnomonique"